《2025年学考A加同步课时练八年级数学下册人教版》

1.若三角形的三条中位线长分别为2 cm，3 cm，4 cm，则原三角形的周长为（ ）
A. 4.5 cm
B. 18 cm
C. 9 cm
D. 36 cm

答案： B

2.如图，DE是△ABC的中位线，若BC = 8，则DE的长为（ ）
A. 2 B. 4 C. 6 D. 8
　　　　　　　 　　　

答案： B

3.如图，DE是△ABC的中位线，F是DE的中点，CF的延长线交AB于点G，若△CEF的面积为12 cm²，则S△DGF的值为（ ）


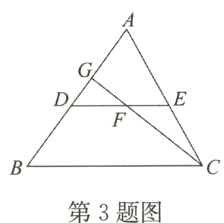
A. 4 cm²
B. 6 cm²
C. 8 cm²
D. 9 cm²

答案：
A　[解析]如图,取CG的中点H,连接EH,
∵E是AC的中点，
∴EH是△ACG的中位线，
∴EH//AD,
∴∠GDF =∠HEF;
∵F是DE的中点，
∴DF = EF,
在△DFG和△EFH中，
$\left\{\begin{array}{l} \angle GDF=\angle HEF,\\ DF = EF,\\ \angle DFG=\angle EFH,\end{array}\right. $
∴△DFG≌△EFH(ASA),
∴FG = FH,$S_{\triangle EFH}=S_{\triangle DGF}$.
又
∵FC = FH + HC = FH + GH = FH + FG + FH = 3FH,
∴$S_{\triangle CEF}=3S_{\triangle EFH}$,
∴$S_{\triangle CEF}=3S_{\triangle DGF}$,
∴$S_{\triangle DGF}=\frac{1}{3}\times12 = 4(cm^{2})$.
故选A.

4.如图，已知在△ABC中，D，E分别是AB，AC的中点，BC = 6 cm，则DE的长度是_______cm.
　

答案： 3

5.如图，在△ABC中，AB = 13，BC = 12，点D，E分别是AB，BC的中点，连接DE，CD，如果DE = 2.5，那么△ACD的周长是_______.
　　　

答案： 18　[解析]
∵D,E分别是AB,BC的中点，
∴AC = 2DE = 5,AC//DE,
$AC^{2}+BC^{2}=5^{2}+12^{2}=169$,
$AB^{2}=13^{2}=169$,
∴$AC^{2}+BC^{2}=AB^{2}$,
∴∠ACB = 90°.
∵AC//DE,
∴∠DEB = 90°，又
∵E是BC的中点，
∴直线DE是线段BC的垂直平分线，
∴DC = BD,
∴△ACD的周长 = AC + AD + CD = AC + AD + BD = AC + AB = 18.
故答案为18.

6.如图，在△MBN中，已知BM = 6，BN = 7，MN = 10，点A，C，D分别是MB，NB，MN的中点，则四边形ABCD的周长是_______.
　　　

答案： 13　[解析]
∵A,C,D分别是各边中点，
∴$AB=\frac{1}{2}BM=\frac{1}{2}\times6 = 3$;
$BC=\frac{1}{2}BN=\frac{1}{2}\times7=\frac{7}{2}$;
$AD=\frac{1}{2}BN=\frac{1}{2}\times7=\frac{7}{2}$;
$CD=\frac{1}{2}BM=\frac{1}{2}\times6 = 3$.
四边形ABCD的周长是AD + AB + BC + CD = $\frac{7}{2}+3+\frac{7}{2}+3 = 13$.
故答案为13.