2025年学考A加同步课时练八年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学考A加同步课时练八年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
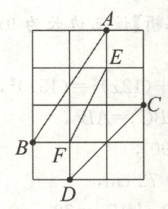
9. 如图,在4×3的正方形网格中,每个小正方形的边长都是1.
(1)分别求出线段AB,CD的长度;
(2)在图中画线段EF,使得$EF=\sqrt{5}$,以AB,CD,EF三条线段长为边能否构成直角三角形,并说明理由.

(1)分别求出线段AB,CD的长度;
(2)在图中画线段EF,使得$EF=\sqrt{5}$,以AB,CD,EF三条线段长为边能否构成直角三角形,并说明理由.

答案:
解:
(1)$AB=\sqrt{3^{2}+2^{2}}=\sqrt{13},CD=\sqrt{2^{2}+2^{2}}=2\sqrt{2}$.
(2)如图,$EF=\sqrt{2^{2}+1^{2}}=\sqrt{5}$,$\because CD^{2}+EF^{2}=8 + 5 = 13,AB^{2}=13$,$\therefore CD^{2}+EF^{2}=AB^{2}$,$\therefore$以$AB,CD,EF$三条线可以组成直角三角形.
解:
(1)$AB=\sqrt{3^{2}+2^{2}}=\sqrt{13},CD=\sqrt{2^{2}+2^{2}}=2\sqrt{2}$.
(2)如图,$EF=\sqrt{2^{2}+1^{2}}=\sqrt{5}$,$\because CD^{2}+EF^{2}=8 + 5 = 13,AB^{2}=13$,$\therefore CD^{2}+EF^{2}=AB^{2}$,$\therefore$以$AB,CD,EF$三条线可以组成直角三角形.

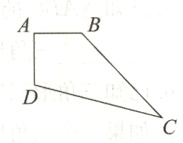
10. 如图,已知在四边形ABCD中,$\angle A = 90^{\circ},AB = 2$ cm,$AD=\sqrt{5}$ cm,$CD = 5$ cm,$BC = 4$ cm,求四边形ABCD的面积.

答案:
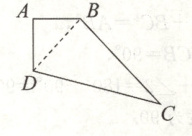
解:连接$BD$. $\because∠A = 90^{\circ},AB = 2\ cm,AD=\sqrt{5}$,$\therefore$根据勾股定理可得$BD = 3$.又$\because CD = 5,BC = 4$,$\therefore CD^{2}=BC^{2}+BD^{2}$,$\therefore\triangle BCD$是直角三角形,$\therefore∠CBD = 90^{\circ}$,$\therefore S_{四边形ABCD}=S_{\triangle ABD}+S_{\triangle BCD}=\frac{1}{2}AB\cdot AD+\frac{1}{2}BC\cdot BD=\frac{1}{2}×2×\sqrt{5}+\frac{1}{2}×4×3=\sqrt{5}+6(cm^{2})$.
解:连接$BD$. $\because∠A = 90^{\circ},AB = 2\ cm,AD=\sqrt{5}$,$\therefore$根据勾股定理可得$BD = 3$.又$\because CD = 5,BC = 4$,$\therefore CD^{2}=BC^{2}+BD^{2}$,$\therefore\triangle BCD$是直角三角形,$\therefore∠CBD = 90^{\circ}$,$\therefore S_{四边形ABCD}=S_{\triangle ABD}+S_{\triangle BCD}=\frac{1}{2}AB\cdot AD+\frac{1}{2}BC\cdot BD=\frac{1}{2}×2×\sqrt{5}+\frac{1}{2}×4×3=\sqrt{5}+6(cm^{2})$.

查看更多完整答案,请扫码查看


