2025年学考A加同步课时练八年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学考A加同步课时练八年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
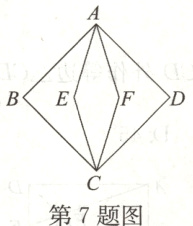
7. 如图,正方形ABCD的面积为18,菱形AECF的面积为6,则菱形的边长为________.

答案:
$\sqrt{10}$ 【解析】因为正方形ABCD的面积为18,
所以AC = $\sqrt{18}\times\sqrt{2}=6$,
因为菱形AECF的面积为6,
所以EF = $\frac{2\times6}{6}=2$,
所以菱形的边长 = $\sqrt{1^{2}+3^{2}}=\sqrt{10}$.
故答案为$\sqrt{10}$.

$\sqrt{10}$ 【解析】因为正方形ABCD的面积为18,
所以AC = $\sqrt{18}\times\sqrt{2}=6$,
因为菱形AECF的面积为6,
所以EF = $\frac{2\times6}{6}=2$,
所以菱形的边长 = $\sqrt{1^{2}+3^{2}}=\sqrt{10}$.
故答案为$\sqrt{10}$.

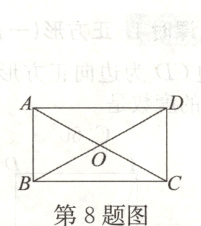
8. 如图,在矩形ABCD中,对角线AC,BD交于点O,要使矩形ABCD成为正方形,应添加的一个条件是________.

答案:
AB = BC(答案不唯一)
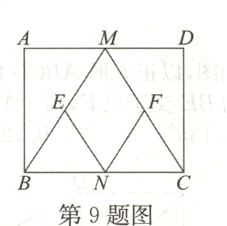
9. 如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是边BM,CM的中点,当AB∶AD=________时,四边形MENF是正方形.

答案:
1∶2 【解析】当AB∶AD = 1∶2时,四边形MENF是正方形,
理由是:
∵AB∶AD = 1∶2,AM = DM,AB = CD,
∴AB = AM = DM = DC,
∵∠A = ∠D = 90°,
∴∠ABM = ∠AMB = ∠DMC = ∠DCM = 45°,
∴∠BMC = 90°,
∵四边形ABCD是矩形,
∴∠ABC = ∠DCB = 90°,
∴∠MBC = ∠MCB = 45°,
∴BM = CM.
∵N,E,F分别是BC,BM,CM的中点,
∴BE = CF,ME = MF,NF//BM,NE//CM,
∴四边形MENF是平行四边形.
∵ME = MF,∠BMC = 90°,
∴四边形MENF是正方形.
即当AB∶AD = 1∶2时,四边形MENF是正方形,
故答案为1∶2.
理由是:
∵AB∶AD = 1∶2,AM = DM,AB = CD,
∴AB = AM = DM = DC,
∵∠A = ∠D = 90°,
∴∠ABM = ∠AMB = ∠DMC = ∠DCM = 45°,
∴∠BMC = 90°,
∵四边形ABCD是矩形,
∴∠ABC = ∠DCB = 90°,
∴∠MBC = ∠MCB = 45°,
∴BM = CM.
∵N,E,F分别是BC,BM,CM的中点,
∴BE = CF,ME = MF,NF//BM,NE//CM,
∴四边形MENF是平行四边形.
∵ME = MF,∠BMC = 90°,
∴四边形MENF是正方形.
即当AB∶AD = 1∶2时,四边形MENF是正方形,
故答案为1∶2.
10. 如图,四边形ABCD和四边形CEFG都是正方形,且BC=CD,CE=CG,∠BCD=∠GCE=90°.
(1)求证:△BCG≌△DCE;
(2)求证:BG⊥DE.
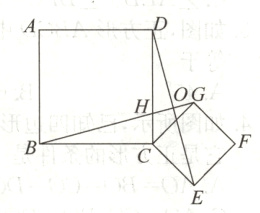
(1)求证:△BCG≌△DCE;
(2)求证:BG⊥DE.

答案:
证明:
(1)
∵∠BCD = ∠GCE = 90°,
∴∠BCG = ∠DCE,
在△BCG与△DCE中,
$\begin{cases}BC = CD,\\\angle BCG=\angle DCE,\\CE = CG,\end{cases}$
∴△BCG≌△DCE(SAS).
(2)
∵△BCG≌△DCE,
∴∠HBC = ∠ODH,
∵∠HBC + ∠BHC = 90°,∠BHC = ∠DHO,
∴∠ODH + ∠DHO = 90°,
∴∠DOH = 90°,
∴BG⊥DE.
(1)
∵∠BCD = ∠GCE = 90°,
∴∠BCG = ∠DCE,
在△BCG与△DCE中,
$\begin{cases}BC = CD,\\\angle BCG=\angle DCE,\\CE = CG,\end{cases}$
∴△BCG≌△DCE(SAS).
(2)
∵△BCG≌△DCE,
∴∠HBC = ∠ODH,
∵∠HBC + ∠BHC = 90°,∠BHC = ∠DHO,
∴∠ODH + ∠DHO = 90°,
∴∠DOH = 90°,
∴BG⊥DE.
11. 如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF//BC交BE的延长线于F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
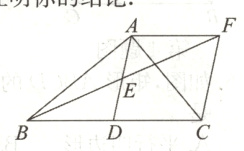
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.

答案:
(1)证明:
∵AF//BC,
∴∠EAF = ∠EDB,
∵E是AD的中点,
∴AE = DE,
在△AEF和△DEB中,
$\begin{cases}\angle EAF=\angle EDB,\\AE = DE,\\\angle AEF=\angle DEB,\end{cases}$
∴△AEF≌△DEB(ASA),
∴AF = BD,
∵在△ABC中,∠BAC = 90°,AD是中线,
∴AD = BD = DC = $\frac{1}{2}$BC,
∴AD = AF.
(2)解:四边形ADCF是正方形.
∵AF = BD = DC,AF//BC,
∴四边形ADCF是平行四边形,
∵AB = AC,AD是中线,
∴AD⊥BC,
∵AD = AF,
∴四边形ADCF是正方形.
(1)证明:
∵AF//BC,
∴∠EAF = ∠EDB,
∵E是AD的中点,
∴AE = DE,
在△AEF和△DEB中,
$\begin{cases}\angle EAF=\angle EDB,\\AE = DE,\\\angle AEF=\angle DEB,\end{cases}$
∴△AEF≌△DEB(ASA),
∴AF = BD,
∵在△ABC中,∠BAC = 90°,AD是中线,
∴AD = BD = DC = $\frac{1}{2}$BC,
∴AD = AF.
(2)解:四边形ADCF是正方形.
∵AF = BD = DC,AF//BC,
∴四边形ADCF是平行四边形,
∵AB = AC,AD是中线,
∴AD⊥BC,
∵AD = AF,
∴四边形ADCF是正方形.
查看更多完整答案,请扫码查看


