《2025年学考A加同步课时练八年级数学下册人教版》

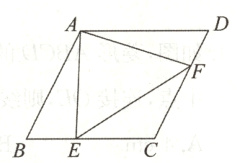
6. 已知:如图,在菱形ABCD中,E,F分别是BC和DC边上的点,且EC=FC.
求证:∠AEF=∠AFE.

答案： 证明:
∵四边形ABCD是菱形，
∴AB = AD，BC = DC，∠B = ∠D，
∵EC = FC，
∴BE = DF.
在△ABE和△ADF中，
$\begin{cases}AB = AD,\\\angle B = \angle D,\\BE = DF,\end{cases}$
∴△ABE≌△ADF(SAS).
∴AE = AF，
∴∠AEF = ∠AFE.

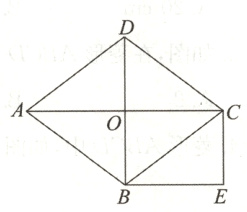
7. 如图,O是菱形ABCD对角线AC与BD的交点,CD=5 cm,OD=3 cm.过点C作CE//DB,过点B作BE//AC,CE与BE相交于点E.
(1)求OC的长;
(2)求四边形OBEC的面积.

答案： 解:
(1)
∵ABCD是菱形，
∴AC⊥BD，
∴直角△OCD中，$OC = \sqrt{CD^{2}-OD^{2}}=\sqrt{5^{2}-3^{2}} = 4(cm)$.
(2)
∵CE//DB，BE//AC，
∴四边形OBEC为平行四边形，
又
∵AC⊥BD，即∠COB = 90°，
∴平行四边形OBEC为矩形，
∵OB = OD，
∴$S_{矩形OBEC}=OB\cdot OC = 4×3 = 12(cm^{2})$.