2025年学考A加同步课时练八年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学考A加同步课时练八年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列各组数中,能构成直角三角形的是 ( )
A. $1,\sqrt{2},\sqrt{2}$
B. 6,8,10
C. 4,5,9
D. 5,12,18
A. $1,\sqrt{2},\sqrt{2}$
B. 6,8,10
C. 4,5,9
D. 5,12,18
答案:
B
2. 下列四组线段中,能组成直角三角形的是 ( )
A. $a = 1,b = 2,c = 3$
B. $a = 4,b = 2,c = 3$
C. $a = 4,b = 2,c = 5$
D. $a = 12,b = 5,c = 13$
A. $a = 1,b = 2,c = 3$
B. $a = 4,b = 2,c = 3$
C. $a = 4,b = 2,c = 5$
D. $a = 12,b = 5,c = 13$
答案:
D
3. 满足下列条件的△ABC,不是直角三角形的是 ( )
A. $b^{2}-c^{2}=a^{2}$
B. $a:b:c = 3:4:5$
C. $\angle C=\angle A-\angle B$
D. $\angle A:\angle B:\angle C = 9:12:15$
A. $b^{2}-c^{2}=a^{2}$
B. $a:b:c = 3:4:5$
C. $\angle C=\angle A-\angle B$
D. $\angle A:\angle B:\angle C = 9:12:15$
答案:
D 【解析】$b^{2}-c^{2}=a^{2}$,则$b^{2}=a^{2}+c^{2}$,$\triangle ABC$是直角三角形;$a:b:c = 3:4:5$,设$a = 3x,b = 4x,c = 5x$,$a^{2}+b^{2}=c^{2}$,$\triangle ABC$是直角三角形;$∠C=∠A - ∠B$,则$∠B=∠A + ∠C$,$∠B = 90^{\circ}$,$\triangle ABC$是直角三角形;$∠A:∠B:∠C = 9:12:15$,设$∠A,∠B,∠C$分别为$9x,12x,15x$,则$9x + 12x + 15x = 180^{\circ}$,解得$x = 5^{\circ}$,则$∠A,∠B,∠C$分别为$45^{\circ},60^{\circ},75^{\circ}$,$\triangle ABC$不是直角三角形.故选 D.
4. 已知一个三角形的三边长分别为a,b,c,且它们满足$(a + b)^{2}-c^{2}=2ab$,则该三角形的形状为 ( )
A. 锐角三角形
B. 直角三角形
C. 钝角三角形
D. 无法确定
A. 锐角三角形
B. 直角三角形
C. 钝角三角形
D. 无法确定
答案:
B 【解析】$\because(a + b)^{2}-c^{2}=2ab$,$\therefore a^{2}+b^{2}=c^{2}$,$\therefore$该三角形为直角三角形.故选 B.
5. 已知△ABC的三边长为a,b,c,满足$a + b = 10,ab = 18,c = 8$,则此三角形为________三角形.
答案:
直角
6. 已知三角形三边长分别是6,8,10,则此三角形的面积为________.
答案:
24 【解析】$\because6^{2}+8^{2}=10^{2}$,$\therefore$此三角形为直角三角形,$\therefore$此三角形的面积为:$\frac{1}{2}×6×8 = 24$.故答案为 24.
7. 如果一个三角形的三边长之比为9:12:15,且周长为72 cm,则它的面积为________$cm^{2}$.
答案:
216 【解析】设三边长为$9x\ cm,12x\ cm,15x\ cm$,$\because(9x)^{2}+(12x)^{2}=(15x)^{2}$,$\therefore AC^{2}+BC^{2}=AB^{2}$,$\therefore∠C = 90^{\circ}$,$\because$周长为$72\ cm$,$\therefore9x + 12x + 15x = 72$,解得$x = 2$,$\therefore9x = 18,12x = 24$,$\therefore$它的面积为:$\frac{1}{2}×18×24 = 216(cm^{2})$,故答案为 216.
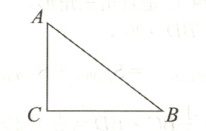
216 【解析】设三边长为$9x\ cm,12x\ cm,15x\ cm$,$\because(9x)^{2}+(12x)^{2}=(15x)^{2}$,$\therefore AC^{2}+BC^{2}=AB^{2}$,$\therefore∠C = 90^{\circ}$,$\because$周长为$72\ cm$,$\therefore9x + 12x + 15x = 72$,解得$x = 2$,$\therefore9x = 18,12x = 24$,$\therefore$它的面积为:$\frac{1}{2}×18×24 = 216(cm^{2})$,故答案为 216.

8. 如图,三个正方形的面积分别为$S_{1}=3,S_{2}=2,S_{3}=1$,则分别以它们的一边为边围成的三角形中,$\angle 1+\angle 2=$________度.
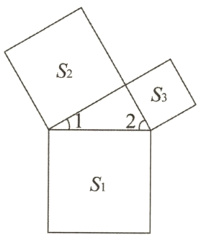

答案:
90 【解析】$\because S_{1}=3,S_{2}=2,S_{3}=1$,$\therefore AC^{2}+BC^{2}=AB^{2}$,$\therefore∠ACB = 90^{\circ}$,$\therefore∠1 + ∠2 = 180^{\circ}-90^{\circ}=90^{\circ}$.故答案为 90.
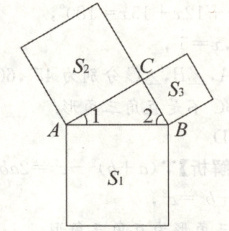
90 【解析】$\because S_{1}=3,S_{2}=2,S_{3}=1$,$\therefore AC^{2}+BC^{2}=AB^{2}$,$\therefore∠ACB = 90^{\circ}$,$\therefore∠1 + ∠2 = 180^{\circ}-90^{\circ}=90^{\circ}$.故答案为 90.

查看更多完整答案,请扫码查看


