2025年学考A加同步课时练八年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学考A加同步课时练八年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )
A. a = 1,b = 2,c = 3
B. a = 7,b = 24,c = 25
C. a = 6,b = 8,c = 10
D. a = 3,b = 4,c = 5
A. a = 1,b = 2,c = 3
B. a = 7,b = 24,c = 25
C. a = 6,b = 8,c = 10
D. a = 3,b = 4,c = 5
答案:
A
2. 在△ABC中,AB = $\sqrt{2}$,BC = $\sqrt{5}$,AC = $\sqrt{3}$,则( )
A. ∠A = 90°
B. ∠B = 90°
C. ∠C = 90°
D. ∠A = ∠B
A. ∠A = 90°
B. ∠B = 90°
C. ∠C = 90°
D. ∠A = ∠B
答案:
A
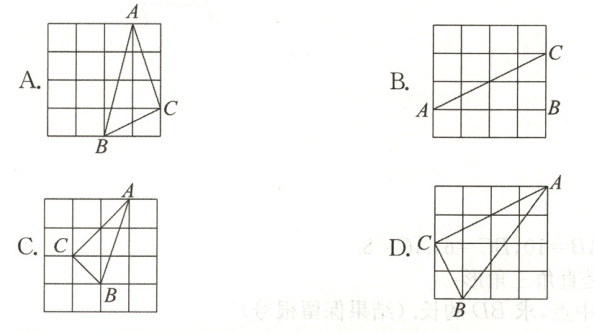
3. 如图,在四个均由十六个小正方形组成的正方形网格中,各有一个三角形 ABC,那么这四个三角形中,不是直角三角形的是( )

答案:
A [解析]A.三角形各边长为$\sqrt{17}$,$\sqrt{10}$,$\sqrt{5}$,$(\sqrt{5})^{2}+(\sqrt{10})^{2}<(\sqrt{17})^{2}$,故该三角形为钝角三角形;
B.各边长2,4,$2\sqrt{5}$,$2^{2}+4^{2}=(2\sqrt{5})^{2}$,故该三角形为直角三角形;
C.各边长$\sqrt{2}$,$\sqrt{8}$,$\sqrt{10}$,$(\sqrt{2})^{2}+(\sqrt{8})^{2}=(\sqrt{10})^{2}$,故该三角形为直角三角形;
D.各边长$\sqrt{5}$,$2\sqrt{5}$,5,$(\sqrt{5})^{2}+(2\sqrt{5})^{2}=(5)^{2}$,故该三角形为直角三角形.
故选A.
B.各边长2,4,$2\sqrt{5}$,$2^{2}+4^{2}=(2\sqrt{5})^{2}$,故该三角形为直角三角形;
C.各边长$\sqrt{2}$,$\sqrt{8}$,$\sqrt{10}$,$(\sqrt{2})^{2}+(\sqrt{8})^{2}=(\sqrt{10})^{2}$,故该三角形为直角三角形;
D.各边长$\sqrt{5}$,$2\sqrt{5}$,5,$(\sqrt{5})^{2}+(2\sqrt{5})^{2}=(5)^{2}$,故该三角形为直角三角形.
故选A.
4. 甲、乙两艘客轮同时离开港口,航行的速度都是40 m/min,甲客轮用15 min到达点A,乙客轮用20 min到达点B,若A,B两点的直线距离为1 000 m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
A. 北偏西30°
B. 南偏西30°
C. 南偏东60°
D. 南偏西60°
A. 北偏西30°
B. 南偏西30°
C. 南偏东60°
D. 南偏西60°
答案:
4.C [解析]甲的路程:$40×15 = 600$m,乙的路程:$20×40 = 800$m,
$\because600^{2}+800^{2}=1000^{2}$,
$\therefore$甲和乙两艘轮船的行驶路线呈垂直关系,
$\because$甲客轮沿着北偏东$30^{\circ}$,
$\therefore$乙客轮的航行方向可能是南偏东$60^{\circ}$.故选C.
$\because600^{2}+800^{2}=1000^{2}$,
$\therefore$甲和乙两艘轮船的行驶路线呈垂直关系,
$\because$甲客轮沿着北偏东$30^{\circ}$,
$\therefore$乙客轮的航行方向可能是南偏东$60^{\circ}$.故选C.
5. 如图,已知△ABC中,AB = 10,AC = 8,BC = 6,DE是AC的垂直平分线,DE交AB于点D,连接CD,则CD = ________.


答案:
5
6. 如图,AC = 6,BC = 8,AB = 10,则点C到线段AB的距离是________.


答案:
4.8
7. 如图,在四边形ABCD中,∠ABC = 90°,AB = 3,BC = 4,CD = 5,DA = 5$\sqrt{2}$,则BD的长为________.
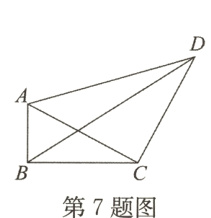

答案:
$\sqrt{65}$ [解析]作$DM\perp BC$,交$BC$延长线于$M$,如图所示:
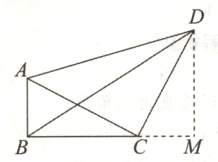
则$\angle M = 90^{\circ}$,
$\therefore\angle DCM+\angle CDM = 90^{\circ}$.
$\because\angle ABC = 90^{\circ}$,$AB = 3$,$BC = 4$,
$\therefore AC^{2}=AB^{2}+BC^{2}=25$,
$\therefore AC = 5$,
$\because AD = 5\sqrt{2}$,$CD = 5$,
$\therefore AC^{2}+CD^{2}=AD^{2}$,
$\therefore\triangle ACD$是直角三角形,$\angle ACD = 90^{\circ}$,
$\therefore\angle ACB+\angle DCM = 90^{\circ}$,
$\therefore\angle ACB=\angle CDM$,
$\because\angle ABC=\angle M = 90^{\circ}$,
在$\triangle ABC$和$\triangle CMD$中,
$\begin{cases}\angle ACB=\angle CDM,\\\angle ABC=\angle M,\\AC = CD = 5,\end{cases}$
$\therefore\triangle ABC\cong\triangle CMD$,
$\therefore CM = AB = 3$,$DM = BC = 4$,
$\therefore BM = BC + CM = 7$,
$\therefore BD=\sqrt{BM^{2}+DM^{2}}=\sqrt{7^{2}+4^{2}}=\sqrt{65}$.
故答案为$\sqrt{65}$.
$\sqrt{65}$ [解析]作$DM\perp BC$,交$BC$延长线于$M$,如图所示:

则$\angle M = 90^{\circ}$,
$\therefore\angle DCM+\angle CDM = 90^{\circ}$.
$\because\angle ABC = 90^{\circ}$,$AB = 3$,$BC = 4$,
$\therefore AC^{2}=AB^{2}+BC^{2}=25$,
$\therefore AC = 5$,
$\because AD = 5\sqrt{2}$,$CD = 5$,
$\therefore AC^{2}+CD^{2}=AD^{2}$,
$\therefore\triangle ACD$是直角三角形,$\angle ACD = 90^{\circ}$,
$\therefore\angle ACB+\angle DCM = 90^{\circ}$,
$\therefore\angle ACB=\angle CDM$,
$\because\angle ABC=\angle M = 90^{\circ}$,
在$\triangle ABC$和$\triangle CMD$中,
$\begin{cases}\angle ACB=\angle CDM,\\\angle ABC=\angle M,\\AC = CD = 5,\end{cases}$
$\therefore\triangle ABC\cong\triangle CMD$,
$\therefore CM = AB = 3$,$DM = BC = 4$,
$\therefore BM = BC + CM = 7$,
$\therefore BD=\sqrt{BM^{2}+DM^{2}}=\sqrt{7^{2}+4^{2}}=\sqrt{65}$.
故答案为$\sqrt{65}$.
查看更多完整答案,请扫码查看


