《2025年学考A加同步课时练八年级数学下册人教版》

1. 直角三角形两条直角边的长分别为3和4，则斜边长为（ ）
A. 4
B. 5
C. 6
D. 10

答案： B

2. 若等腰三角形的腰长为10，底边长为12，则底边上的高为（ ）
A. 6
B. 7
C. 8
D. 9

答案： C

3. 如图1是边长为1的六个小正方形组成的图形，它可以围成图2的正方体，则图1中小正方形顶点A，B在围成的正方体上的距离是（ ）


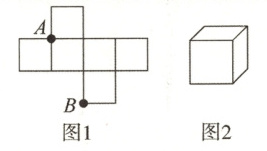
A. 0
B. 1
C.$\sqrt{2}$
D.$\sqrt{3}$

答案： B

4. 若一个直角三角形的面积为6 cm²，斜边长为5 cm，则该直角三角形的周长为________cm².

答案： 12　[解析]设直角三角形的两直角边长分别为a,b,
　则$\frac{1}{2}$ab=6,即ab=12,
　由勾股定理得，$a^{2}+b^{2}=25$,
　则$(a+b)^{2}-2ab=25$,
解得a+b=7,
∴该直角三角形的周长=a+b+c=12.故答案为12.

5. 直角三角形的周长为12 cm，斜边长为5 cm，则斜边上的高是________cm.

答案： 2.4[解析]设另外两直角边分别为x,y.则x+y=12−5=7①,
　$x^{2}+y^{2}=25$②,
　①②联立解得xy=12,
　故直角三角形的面积$\frac{1}{2}$xy=6,
　设斜边上的高为h,则$5h\times\frac{1}{2}=6$,
　解得h=2.4.
　故答案为2.4.

6. 如图，三个正方形中，其中两个正方形的面积分别是100，36，则字母A所代表的正方形的边长是________.

答案： 8　[解析]面积是100的正方形的边长为10，面积是36的正方形的边长为6，
∴字母A所代表的正方形的边长=$\sqrt{10^{2}-6^{2}} = 8$.
　故答案为8.

7. 如图，平面直角坐标系中的每个小正方形边长为1，△ABC的顶点在网格的格点上.
(1)画线段AD//BC，且使AD=BC，连接BD，此时D点的坐标是________；
(2)直接写出线段AC的长为________，AD的长为________，BD的长为________；
(3)直接写出△ABD为________三角形，四边形ADBC面积是________.

答案：

(1)(0,−4)　
(2)$\sqrt{10}$　$2\sqrt{10}$　$\sqrt{10}$　
(3)直角　20　[解析]
(1)如图所示:D 点的坐标是(0，−4).
　　　　
(2)线段AC的长为$\sqrt{3^{2}+1^{2}}=\sqrt{10}$,AD 的长为$\sqrt{6^{2}+2^{2}} = 2\sqrt{10}$,BD的长为$\sqrt{3^{2}+1^{2}}=\sqrt{10}$
(3)
∵$AB=\sqrt{5^{2}+5^{2}} = 5\sqrt{2}$,$AD = 2\sqrt{10}$,$BD=\sqrt{10}$,
　$(2\sqrt{10})^{2}+(\sqrt{10})^{2}=(5\sqrt{2})^{2}$,
∴△ABD为直角三角形，四边形ADBC 面积是$2\sqrt{10}\times\sqrt{10}=20$.