2025年快乐暑假天天练七年级综合河南专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年快乐暑假天天练七年级综合河南专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列方程中,解是$x= 1$的是 (
A.$2x-3= 1$
B.$2x+3= 1$
C.$1.5= 1-\frac {x}{2}$
D.$3x-4= -x$
D
)A.$2x-3= 1$
B.$2x+3= 1$
C.$1.5= 1-\frac {x}{2}$
D.$3x-4= -x$
答案:
【解析】:
A选项:将$x=1$代入方程$2x-3=1$,得到$2×1-3=-1$,显然$-1\ne1$,所以$x=1$不是该方程的解,故A选项错误;
B选项:将$x=1$代入方程$2x+3=1$,得到$2×1+3=5$,显然$5\ne1$,所以$x=1$不是该方程的解,故B选项错误;
C选项:将$x=1$代入方程$1.5=1-\frac{x}{2}$,得到$1.5=1-\frac{1}{2}$,即$1.5\ne0.5$,所以$x=1$不是该方程的解,故C选项错误;
D选项:将$x=1$代入方程$3x-4=-x$,得到$3×1-4=-1$,且$-1=-1$,等式成立,所以$x=1$是该方程的解,故D选项正确。
【答案】:D
A选项:将$x=1$代入方程$2x-3=1$,得到$2×1-3=-1$,显然$-1\ne1$,所以$x=1$不是该方程的解,故A选项错误;
B选项:将$x=1$代入方程$2x+3=1$,得到$2×1+3=5$,显然$5\ne1$,所以$x=1$不是该方程的解,故B选项错误;
C选项:将$x=1$代入方程$1.5=1-\frac{x}{2}$,得到$1.5=1-\frac{1}{2}$,即$1.5\ne0.5$,所以$x=1$不是该方程的解,故C选项错误;
D选项:将$x=1$代入方程$3x-4=-x$,得到$3×1-4=-1$,且$-1=-1$,等式成立,所以$x=1$是该方程的解,故D选项正确。
【答案】:D
2. 下列方程组中是二元一次方程组的是 (
A.$\left\{\begin{array}{l} 3x-2y= 1,\\ 3x+1= 5\end{array} \right. $
B.$\left\{\begin{array}{l} x-y= 2,\\ xy= 1\end{array} \right. $
C.$\left\{\begin{array}{l} 3x-y= 2,\\ \frac {2}{x}+\frac {3}{y}= 1\end{array} \right. $
D.$\left\{\begin{array}{l} 3x-y= 1,\\ 3x+z= 7\end{array} \right. $
A
)A.$\left\{\begin{array}{l} 3x-2y= 1,\\ 3x+1= 5\end{array} \right. $
B.$\left\{\begin{array}{l} x-y= 2,\\ xy= 1\end{array} \right. $
C.$\left\{\begin{array}{l} 3x-y= 2,\\ \frac {2}{x}+\frac {3}{y}= 1\end{array} \right. $
D.$\left\{\begin{array}{l} 3x-y= 1,\\ 3x+z= 7\end{array} \right. $
答案:
【解析】:
A. 方程组中有两个方程,且只涉及两个未知数$x$和$y$,所有未知数的次数都是1,满足二元一次方程组的定义。
B. 第一个方程是二元一次方程,但第二个方程$xy=1$中,未知数的次数是2(因为$x$和$y$相乘),所以不满足二元一次方程组的定义。
C. 第一个方程是二元一次方程,但第二个方程$\frac {2}{x}+\frac {3}{y}= 1$中,未知数出现在分母位置,不是一次方程,所以不满足二元一次方程组的定义。
D. 方程组中有两个方程,但涉及三个未知数$x$,$y$和$z$,所以不满足二元一次方程组的定义(二元一次方程组应只包含两个未知数)。
【答案】:A
A. 方程组中有两个方程,且只涉及两个未知数$x$和$y$,所有未知数的次数都是1,满足二元一次方程组的定义。
B. 第一个方程是二元一次方程,但第二个方程$xy=1$中,未知数的次数是2(因为$x$和$y$相乘),所以不满足二元一次方程组的定义。
C. 第一个方程是二元一次方程,但第二个方程$\frac {2}{x}+\frac {3}{y}= 1$中,未知数出现在分母位置,不是一次方程,所以不满足二元一次方程组的定义。
D. 方程组中有两个方程,但涉及三个未知数$x$,$y$和$z$,所以不满足二元一次方程组的定义(二元一次方程组应只包含两个未知数)。
【答案】:A
3. 如图,在$△ABC$中,D 是 BC 延长线上一点,$∠B= 40^{\circ },$$∠ACD= 120^{\circ }$,则$∠A$等于 (
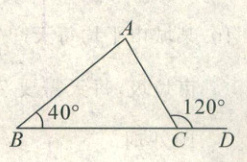
A.$60^{\circ }$
B.$70^{\circ }$
C.$80^{\circ }$
D.$90^{\circ }$
C
)
A.$60^{\circ }$
B.$70^{\circ }$
C.$80^{\circ }$
D.$90^{\circ }$
答案:
【解析】:
根据三角形的外角性质,三角形的一个外角等于与它不相邻的两个内角之和。
在本题中,$\angle ACD$是$\triangle ABC$的一个外角,因此有:
$\angle ACD = \angle A + \angle B$。
已知$\angle B = 40^\circ$和$\angle ACD = 120^\circ$,代入上式得:
$120^\circ = \angle A + 40^\circ$。
解这个方程,得到:
$\angle A = 120^\circ - 40^\circ = 80^\circ$。
【答案】:C
根据三角形的外角性质,三角形的一个外角等于与它不相邻的两个内角之和。
在本题中,$\angle ACD$是$\triangle ABC$的一个外角,因此有:
$\angle ACD = \angle A + \angle B$。
已知$\angle B = 40^\circ$和$\angle ACD = 120^\circ$,代入上式得:
$120^\circ = \angle A + 40^\circ$。
解这个方程,得到:
$\angle A = 120^\circ - 40^\circ = 80^\circ$。
【答案】:C
4. 若$\frac {3}{2}a^{x-y}b^{2}与-8ab^{2x}$是同类项,则$x+y$的值是 (
A.-1
B.0
C.1
D.2
C
)A.-1
B.0
C.1
D.2
答案:
【解析】:
由于$\frac {3}{2}a^{x-y}b^{2}$与$-8ab^{2x}$是同类项,根据同类项的定义,它们的字母部分(包括字母和指数)必须完全相同。
因此,我们可以列出以下方程组来找出$x$和$y$的值:
$\begin{cases}x - y = 1 \quad (1) \\2x = 2 \quad (2)\end{cases}$
从方程
(2)我们可以解出$x$:
$2x = 2 \implies x = 1$
将$x = 1$代入方程
(1)中,我们可以解出$y$:
$1 - y = 1 \implies y = 0$
现在我们找到了$x$和$y$的值,我们可以找到$x+y$的值:
$x+y = 1+0 = 1$
【答案】:C
由于$\frac {3}{2}a^{x-y}b^{2}$与$-8ab^{2x}$是同类项,根据同类项的定义,它们的字母部分(包括字母和指数)必须完全相同。
因此,我们可以列出以下方程组来找出$x$和$y$的值:
$\begin{cases}x - y = 1 \quad (1) \\2x = 2 \quad (2)\end{cases}$
从方程
(2)我们可以解出$x$:
$2x = 2 \implies x = 1$
将$x = 1$代入方程
(1)中,我们可以解出$y$:
$1 - y = 1 \implies y = 0$
现在我们找到了$x$和$y$的值,我们可以找到$x+y$的值:
$x+y = 1+0 = 1$
【答案】:C
5. 下列图形中,对称轴条数最少的是 (
A.等边三角形
B.长方形
C.正方形
D.圆
B
)A.等边三角形
B.长方形
C.正方形
D.圆
答案:
【解析】:
A项等边三角形有三条对称轴,分别为三条边的中垂线;
B项长方形有两条对称轴,分别为两条对边中点连接的线;
C项正方形有四条对称轴,分别为两条对角线以及两条对边中点连接的线;
D项圆有无数条对称轴,任何经过圆心的直线都是其对称轴。
比较各图形的对称轴数量,等边三角形有三条,长方形有两条,正方形有四条,圆有无数条。
因此,对称轴数量最少的是长方形,只有两条。
【答案】:B
A项等边三角形有三条对称轴,分别为三条边的中垂线;
B项长方形有两条对称轴,分别为两条对边中点连接的线;
C项正方形有四条对称轴,分别为两条对角线以及两条对边中点连接的线;
D项圆有无数条对称轴,任何经过圆心的直线都是其对称轴。
比较各图形的对称轴数量,等边三角形有三条,长方形有两条,正方形有四条,圆有无数条。
因此,对称轴数量最少的是长方形,只有两条。
【答案】:B
6. 方程$3x-36= 0$的解为
$x = 12$
.
答案:
【解析】:
给定方程为 $3x - 36 = 0$。
首先,将方程中的常数项移至等式的右侧,得到:
$3x = 36$
然后,将方程两边同时除以3,得到:
$x = 12$
【答案】:$x = 12$
给定方程为 $3x - 36 = 0$。
首先,将方程中的常数项移至等式的右侧,得到:
$3x = 36$
然后,将方程两边同时除以3,得到:
$x = 12$
【答案】:$x = 12$
7. 在$△ABC$中,已知$∠A= 60^{\circ }$,再添加一个条件
AB=AC
,就能使$△ABC$是等边三角形(题中横线上只需写出一个条件即可).
答案:
【解析】:在三角形中,有一个角是60°的等腰三角形是等边三角形。已知∠A=60°,若添加AB=AC,则△ABC是等腰三角形,且顶角为60°,所以△ABC是等边三角形。(答案不唯一,也可添加AB=BC或AC=BC,或∠B=60°,∠C=60°等)
【答案】:AB=AC
【答案】:AB=AC
8. a,b,c 分别是三角形的三边,化简:$|a-b-c|+|b-c-a|-|c-a+b|= $
a - b + c
.
答案:
【解析】:根据三角形三边关系,任意两边之和大于第三边,可得:
$a < b + c$,则 $a - b - c < 0$,所以$|a - b - c| = -(a - b - c) = b + c - a$;
$b < c + a$,则 $b - c - a < 0$,所以$|b - c - a| = -(b - c - a) = c + a - b$;
$c + b > a$(即$c - a + b > 0$),所以$|c - a + b| = c - a + b$。
将上述结果代入原式:
$\begin{aligned}&|a - b - c| + |b - c - a| - |c - a + b|\\=&(b + c - a) + (c + a - b) - (c - a + b)\\=&b + c - a + c + a - b - c + a - b\\=&(b - b - b) + (c + c - c) + (-a + a + a)\\=&-b + c + a\\=&a - b + c\end{aligned}$
【答案】:a - b + c
$a < b + c$,则 $a - b - c < 0$,所以$|a - b - c| = -(a - b - c) = b + c - a$;
$b < c + a$,则 $b - c - a < 0$,所以$|b - c - a| = -(b - c - a) = c + a - b$;
$c + b > a$(即$c - a + b > 0$),所以$|c - a + b| = c - a + b$。
将上述结果代入原式:
$\begin{aligned}&|a - b - c| + |b - c - a| - |c - a + b|\\=&(b + c - a) + (c + a - b) - (c - a + b)\\=&b + c - a + c + a - b - c + a - b\\=&(b - b - b) + (c + c - c) + (-a + a + a)\\=&-b + c + a\\=&a - b + c\end{aligned}$
【答案】:a - b + c
查看更多完整答案,请扫码查看


