2025年学考A加同步课时练八年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学考A加同步课时练八年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 在下列二次根式中,x的取值范围是x>3的是( )
A.$\sqrt{3 - x}$
B.$\sqrt{x + 3}$
C.$\sqrt{x - 3}$
D.$\sqrt{\frac{1}{x - 3}}$
A.$\sqrt{3 - x}$
B.$\sqrt{x + 3}$
C.$\sqrt{x - 3}$
D.$\sqrt{\frac{1}{x - 3}}$
答案:
D
2. 如果代数式$\frac{\sqrt{x}}{\sqrt{x - 1}}$有意义,那么x的取值范围是( )
A.x≥0
B.x≠1
C.x>1
D.x≥0且x≠1
A.x≥0
B.x≠1
C.x>1
D.x≥0且x≠1
答案:
C
3. 化简$\sqrt{9}$的结果是( )
A.3
B. - 3
C.±3
D.9
A.3
B. - 3
C.±3
D.9
答案:
A
4. 若$\sqrt{a^{2}}+a = 0$,则a的取值范围是( )
A.a≥0
B.a≤0
C.a = 0
D.a≠0
A.a≥0
B.a≤0
C.a = 0
D.a≠0
答案:
B
5. 下列等式正确的是( )
A.$(\sqrt{3})^{2}=3$
B.$\sqrt{(-3)^{2}}=-3$
C.$\sqrt{3^{3}}=3$
D.$(-\sqrt{3})^{2}=-3$
A.$(\sqrt{3})^{2}=3$
B.$\sqrt{(-3)^{2}}=-3$
C.$\sqrt{3^{3}}=3$
D.$(-\sqrt{3})^{2}=-3$
答案:
A [解析]($\sqrt{3}$)²=3,A正确;
$\sqrt{(-3)^{2}}=3$,B错误;
$\sqrt{3^{3}}=\sqrt{27}=3\sqrt{3}$,C错误;
$(-\sqrt{3})^{2}=3$,D错误.
故选A.
$\sqrt{(-3)^{2}}=3$,B错误;
$\sqrt{3^{3}}=\sqrt{27}=3\sqrt{3}$,C错误;
$(-\sqrt{3})^{2}=3$,D错误.
故选A.
6. 要使$\sqrt{x + 1}$有意义,则实数x的取值范围是________.
答案:
$x\geqslant -1$
7. 若式子$\frac{\sqrt{x - 2}}{x}$在实数范围内有意义,则x的取值范围是________.
答案:
$x > 0$
8. 若$\sqrt{(a - 2)^{2}}=2 - a$,则a的取值范围是________.
答案:
$a\leqslant 2$
9. 已知实数a在数轴上的位置如图所示,则化简|1 - a| - $\sqrt{a^{2}}$的结果为________.
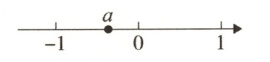
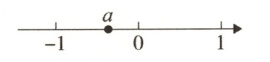
答案:
1 [解析]由数轴可知,$-1 < a < 0$,
∴$1 - a > 0$,
∴原式$=1 - a + a = 1$.
故答案为1.
∴$1 - a > 0$,
∴原式$=1 - a + a = 1$.
故答案为1.
10. 已知$y=\sqrt{1 - 8x}+\sqrt{8x - 1}+2$,求$\sqrt{\frac{x}{y}}+\sqrt{\frac{y}{x}}-2$的值.
答案:
解:由二次根式有意义的条件可知,$1 - 8x = 0$,
解得$x=\frac{1}{8}$.
当$x=\frac{1}{8}$,$y = 2$时,原式$=\sqrt{\frac{1}{16}}+\sqrt{16}-2=\frac{1}{4}+4 - 2=2\frac{1}{4}$.
解得$x=\frac{1}{8}$.
当$x=\frac{1}{8}$,$y = 2$时,原式$=\sqrt{\frac{1}{16}}+\sqrt{16}-2=\frac{1}{4}+4 - 2=2\frac{1}{4}$.
查看更多完整答案,请扫码查看


