2025年优化探究同步导学案高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年优化探究同步导学案高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. (多选)函数$f(x)=(x - 3)e^{x}$在下列区间上单调递增的是(
A.$(-\infty,2)$
B.$(0,3)$
C.$(3,4)$
D.$(2,+\infty)$
CD
)A.$(-\infty,2)$
B.$(0,3)$
C.$(3,4)$
D.$(2,+\infty)$
答案:
1.CD 因为$f^{\prime}(x)=e^{x}+(x - 3)e^{x}=(x - 2)e^{x}$,由$f^{\prime}(x)>0$得$(x - 2)e^{x}>0$,所以$x>2$,所以$f(x)$的单调递增区间为$(2,+\infty)$ ,C,D符合。
2. 已知函数$y = f(x)(x\in R)$的导函数$f'(x)$的图象如图所示,则函数$y = f(x)$(
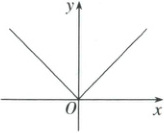
A.在$(-\infty,0)$上单调递减
B.在$(0,+\infty)$上单调递增
C.在$R$上单调递减
D.在$R$上单调递增
D
)
A.在$(-\infty,0)$上单调递减
B.在$(0,+\infty)$上单调递增
C.在$R$上单调递减
D.在$R$上单调递增
答案:
2.D 因为导函数图象在$x$轴及$x$轴上方,则$f^{\prime}(x)\geq0$,函数$f(x)$为增函数,所以$f(x)$在$\mathrm{R}$上递增。
3. 函数$f(x)=x\ln x$的单调递减区间为(
A.$(0,\frac{1}{e})$
B.$(\frac{1}{e},+\infty)$
C.$(-\infty,\frac{1}{e})$
D.$(0,1)$
A
)A.$(0,\frac{1}{e})$
B.$(\frac{1}{e},+\infty)$
C.$(-\infty,\frac{1}{e})$
D.$(0,1)$
答案:
3.A 函数定义域是$(0,+\infty)$,由已知得$f^{\prime}(x)=\ln x + 1$,由$f^{\prime}(x)=\ln x + 1<0$得$0<x<\frac{1}{e}$,所以单调递减区间为$(0,\frac{1}{e})$。
4. 函数$f(x)=x + 2\cos x$,$x\in(0,\pi)$的单调递减区间是
$(\frac{\pi}{6},\frac{5\pi}{6})$
。
答案:
4.答案:$(\frac{\pi}{6},\frac{5\pi}{6})$
解析:由$f^{\prime}(x)=1 - 2\sin x<0$,得$\sin x>\frac{1}{2}$,又$x\in(0,\pi)$,所以$x\in(\frac{\pi}{6},\frac{5\pi}{6})$。
解析:由$f^{\prime}(x)=1 - 2\sin x<0$,得$\sin x>\frac{1}{2}$,又$x\in(0,\pi)$,所以$x\in(\frac{\pi}{6},\frac{5\pi}{6})$。
[例 1] 讨论函数 $f(x)=\frac{1}{2}ax^{2}+x-(a + 1)\ln x$ $(a\geqslant0)$ 的单调性.
[分析] 求导数→对 $a$ 进行分类讨论→每种情况下确定函数在定义域上的单调性.
[分析] 求导数→对 $a$ 进行分类讨论→每种情况下确定函数在定义域上的单调性.
答案:
[例1] [解] 函数$f(x)$的定义域为$(0,+∞)$,$f'(x)=ax + 1 - \frac{a + 1}{x}=\frac{ax^{2}+x-(a + 1)}{x}$
①当$a = 0$时,$f'(x)=\frac{x - 1}{x}$
由$f'(x)>0$,得$x>1$;由$f'(x)<0$,得$0<x<1$。
故$f(x)$在$(0,1)$上单调递减,在$(1,+∞)$上单调递增.
②当$a>0$时,
$f'(x)=\frac{a(x + \frac{a + 1}{a})(x - 1)}{x}$
$\because a>0,\therefore\frac{a + 1}{a}>0$。
由$f'(x)>0$,得$x>1$;由$f'(x)<0$,得$0<x<1$。
故$f'(x)$在$(0,1)$上单调递减,在$(1,+∞)$上单调递增.
综上所述,当$a\geq0$时,$f(x)$在$(0,1)$上单调递减,在$(1,+∞)$上单调递增.
①当$a = 0$时,$f'(x)=\frac{x - 1}{x}$
由$f'(x)>0$,得$x>1$;由$f'(x)<0$,得$0<x<1$。
故$f(x)$在$(0,1)$上单调递减,在$(1,+∞)$上单调递增.
②当$a>0$时,
$f'(x)=\frac{a(x + \frac{a + 1}{a})(x - 1)}{x}$
$\because a>0,\therefore\frac{a + 1}{a}>0$。
由$f'(x)>0$,得$x>1$;由$f'(x)<0$,得$0<x<1$。
故$f'(x)$在$(0,1)$上单调递减,在$(1,+∞)$上单调递增.
综上所述,当$a\geq0$时,$f(x)$在$(0,1)$上单调递减,在$(1,+∞)$上单调递增.
1. 已知函数 $f(x)=\frac{1}{3}x^{3}+\frac{a}{2}x^{2}+(a - 1)x + 1$.
(1)若曲线 $y = f(x)$ 在点 $(1,f(1))$ 处的切线与直线 $8x + 2y + 1 = 0$ 平行,求出这条切线的方程;
(2)求函数 $f(x)$ 的单调区间.
(1)若曲线 $y = f(x)$ 在点 $(1,f(1))$ 处的切线与直线 $8x + 2y + 1 = 0$ 平行,求出这条切线的方程;
(2)求函数 $f(x)$ 的单调区间.
答案:
跟踪训练 1.解:
(1)由题得$f'(x)=x^{2}+ax+(a - 1)$,则$f'(1)=1 + a+(a - 1)=2a$,
$\because y = f(x)$在点$(1,f(1))$处的切线与直线$8x + 2y + 1 = 0$平行,
则$2a=-4$,解得$a=-2$。
又$f(1)=\frac{1}{3}+\frac{a}{2}+(a - 1)+1=-\frac{8}{3}$,
$\therefore$曲线$y = f(x)$在点$(1,f(1))$处的切线为$y+\frac{8}{3}=-4(x - 1)$,即$12x + 3y - 4 = 0$。
(2)$f'(x)=x^{2}+ax+(a - 1)=(x + a - 1)(x + 1)$,
令$f'(x)=0$,得$x=-1$或$x=1 - a$。
①当$1 - a<-1$,即$a>2$时,
$x$ $(-\infty,1 - a)$ $(-1,1 - a)$ $(1 - a,+∞)$
$f'(x)$ $+$ $0$ $-$ $0$ $+$
$f(x)$ 单调递增 $f(1 - a)$ 单调递减 $f(-1)$ 单调递增
②当$1 - a=-1$,即$a = 2$时,$f'(x)\geq0$恒成立,
$f(x)$在$\mathbf{R}$上单调递增,无单调递减区间.
(iii)当$1 - a>-1$,即$a<2$时,
$x$ $(-\infty,-1)$ $(-1,1 - a)$ $(1 - a,+∞)$
$f'(x)$ $+$ $0$ $-$ $0$ $+$
$f(x)$ 单调递增 $f(-1)$ 单调递减 $f(1 - a)$ 单调递增
综上所述,当$a>2$时,$f(x)$的单调递增区间为$(-\infty,1 - a),(-1,+∞)$,单调递减区间为$(1 - a,-1)$;
当$a = 2$时,$f(x)$在$\mathbf{R}$上单调递增,无单调递减区间;
当$a<2$时,$f(x)$的单调递增区间为$(-\infty,-1),(1 - a,+∞)$,单调递减区间为$(-1,1 - a)$。
(1)由题得$f'(x)=x^{2}+ax+(a - 1)$,则$f'(1)=1 + a+(a - 1)=2a$,
$\because y = f(x)$在点$(1,f(1))$处的切线与直线$8x + 2y + 1 = 0$平行,
则$2a=-4$,解得$a=-2$。
又$f(1)=\frac{1}{3}+\frac{a}{2}+(a - 1)+1=-\frac{8}{3}$,
$\therefore$曲线$y = f(x)$在点$(1,f(1))$处的切线为$y+\frac{8}{3}=-4(x - 1)$,即$12x + 3y - 4 = 0$。
(2)$f'(x)=x^{2}+ax+(a - 1)=(x + a - 1)(x + 1)$,
令$f'(x)=0$,得$x=-1$或$x=1 - a$。
①当$1 - a<-1$,即$a>2$时,
$x$ $(-\infty,1 - a)$ $(-1,1 - a)$ $(1 - a,+∞)$
$f'(x)$ $+$ $0$ $-$ $0$ $+$
$f(x)$ 单调递增 $f(1 - a)$ 单调递减 $f(-1)$ 单调递增
②当$1 - a=-1$,即$a = 2$时,$f'(x)\geq0$恒成立,
$f(x)$在$\mathbf{R}$上单调递增,无单调递减区间.
(iii)当$1 - a>-1$,即$a<2$时,
$x$ $(-\infty,-1)$ $(-1,1 - a)$ $(1 - a,+∞)$
$f'(x)$ $+$ $0$ $-$ $0$ $+$
$f(x)$ 单调递增 $f(-1)$ 单调递减 $f(1 - a)$ 单调递增
综上所述,当$a>2$时,$f(x)$的单调递增区间为$(-\infty,1 - a),(-1,+∞)$,单调递减区间为$(1 - a,-1)$;
当$a = 2$时,$f(x)$在$\mathbf{R}$上单调递增,无单调递减区间;
当$a<2$时,$f(x)$的单调递增区间为$(-\infty,-1),(1 - a,+∞)$,单调递减区间为$(-1,1 - a)$。
查看更多完整答案,请扫码查看


