《2025年新坐标同步练习高中数学A版选择性必修第二册人教版青海专用》

典例
(1)如下表,定义函数$f(x)$：

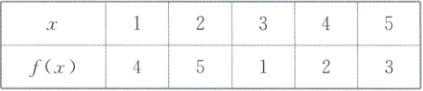
在数列$\{a_{n}\}$中,$a_{1}= 3$,$a_{n}= f(a_{n - 1})(n\geqslant2,n\in\mathbf{N}^{*})$,则$a_{2026}= $3。

答案： 3

(2)已知数列$\{a_{n}\}满足a_{1}= \sqrt{2}$,$a_{n + 1}= \begin{cases}a_{n}-1,a_{n}＞1,\frac{1}{a_{n}},0 ＜ a_{n} ＜ 1,\end{cases} n\in\mathbf{N}^{*}$,则$a_{14}= $$\sqrt{2}-1$。

答案： $\sqrt{2}-1$

练习
在数列$\{a_{n}\}$中,$a_{1}= \frac{1}{2}$,$a_{n}= 1-\frac{1}{a_{n - 1}}(n\geqslant2,n\in\mathbf{N}^{*})$,则$a_{33}=$(D)
A.$\frac{1}{2}$
B.$1$
C.$-1$
D.$2$

答案： D

1. 符合递推公式 $ a_{n}= \sqrt{2}a_{n - 1}(n\geq2,n\in\mathbf{N}^{*}) $ 的数列是(B)
A.$ 1,2,3,4,… $
B.$ 1,\sqrt{2},2,2\sqrt{2},… $
C.$ \sqrt{2},2,\sqrt{2},2,… $
D.$ 0,\sqrt{2},2,2\sqrt{2},… $

答案： 选 B. B 项中相邻的两项，后一项是前一项的√2倍，符合递推公式aₙ=√2aₙ₋₁(n≥2,n∈N*).

2. 已知数列$\{ a_{n}\}满足 a_{1}= 1,a_{n}= a_{n - 1}+2^{n}(n\geq2) $,则$ a_{3}= $(13)
A.$ 3 $
B.$ 5 $
C.$ 11 $
D.$ 13 $

答案： 选 D. 因为a₁=1，aₙ=aₙ₋₁+2ⁿ(n≥2)，所以a₂=a₁+2²=1+4=5，a₃=a₂+2³=5+8=13.

3. 已知$ a_{1}= 1,a_{n}= a_{n - 1}+3(n\geq2,n\in\mathbf{N}^{*}) $,则数列$\{ a_{n}\}$的通项公式为(C)
A.$ a_{n}= 3n + 1 $
B.$ a_{n}= 3n $
C.$ a_{n}= 3n - 2 $
D.$ a_{n}= 3(n - 1) $

答案： 选 C. 因为aₙ=aₙ₋₁+3，所以aₙ - aₙ₋₁=3(n≥2).所以a₂ - a₁=3，a₃ - a₂=3，a₄ - a₃=3，…，aₙ - aₙ₋₁=3，以上各式两边分别相加，得aₙ - a₁=3(n - 1)，所以aₙ=a₁ + 3(n - 1)=1 + 3(n - 1)=3n - 2(n≥2).当n=1时，a₁=1也适合上式，所以aₙ=3n - 2.

4. 已知数列$\{ a_{n}\}的前 n 项和 S_{n}= \frac{4^{n + 1}}{3}-\frac{4}{3}(n\in\mathbf{N}^{*}) $。求数列$\{ a_{n}\}$的通项公式。
解：因为$S_{n}=\frac{4^{n + 1}}{3}-\frac{4}{3}(n\in\mathbf{N}^{*})$，当$n=1$时，$a_{1}=S_{1}=\frac{4^{2}}{3}-\frac{4}{3}=4$，当$n\geq2$时，$a_{n}=S_{n}-S_{n-1}=(\frac{4^{n + 1}}{3}-\frac{4}{3})-(\frac{4^{n}}{3}-\frac{4}{3})=\frac{4^{n + 1}-4^{n}}{3}=\frac{3×4^{n}}{3}=4^{n}$，因为$a_{1}=4$也满足$a_{n}=4^{n}$.综上，$a_{n}=4^{n}(n\in\mathbf{N}^{*})$。

答案： 解：因为Sₙ=4ⁿ⁺¹/3 - 4/3(n∈N*)，当n=1时，a₁=S₁=4²/3 - 4/3=4，当n≥2时，aₙ=Sₙ - Sₙ₋₁=(4ⁿ⁺¹/3 - 4/3)-(4ⁿ/3 - 4/3)=4ⁿ⁺¹ - 4ⁿ/3=3×4ⁿ/3=4ⁿ，因为a₁=4也满足aₙ=4ⁿ.综上，aₙ=4ⁿ(n∈N*).