《2025年新坐标同步练习高中数学A版选择性必修第二册人教版青海专用》

1. 一个等比数列共有 $3m$ 项,若前 $2m$ 项之和为 $15$,后 $2m$ 项之和为 $60$,则这个等比数列的所有项的和为(A)
A.$63$
B.$72$
C.$75$
D.$87$

答案： 解析：选A. 由题意知 $ S_{2m}=15 $, $ S_{3m}-S_{2m}=60 $, 易知 $ S_{m},S_{2m}-S_{m},S_{3m}-S_{2m} $ 成等比数列, 所以 $ (S_{2m}-S_{m})^{2}=S_{m}(S_{3m}-S_{2m}) \Rightarrow S_{m}(S_{m}+60-S_{2m}) $, 解得 $ S_{m}=3 $, 所以 $ S_{3m}=60+3=63 $.

2. 记 $S_{n}$ 为正项等比数列 $\{ a_{n}\}$ 的前 $n$ 项和,若 $S_{3}= 3$,$S_{9}= 21$,则 $S_{6}= $(9)
A.$6$
B.$9$
C.$12$
D.$15$

答案： 解析：选B. 由题意知, $ S_{n}＞0 $, 且 $ S_{3},S_{6}-S_{3},S_{9}-S_{6} $ 成等比数列, 所以 $ (S_{6}-S_{3})^{2}=S_{3}(S_{9}-S_{6}) $, 即 $ (S_{6}-3)^{2}=3(21-S_{6}) $, 解得 $ S_{6}=9 $(负值已舍去).

3. 已知等比数列 $\{ a_{n}\}$ 共有 $2n$ 项,其和为 $-240$,且奇数项的和比偶数项的和大 $80$,则公比 $q= $2.

答案： 解析：由题意, 得 $ \left\{\begin{array}{l} S_{奇}+S_{偶}=-240,\\ S_{奇}-S_{偶}=80,\end{array}\right. $ 解得 $ \left\{\begin{array}{l} S_{奇}=-80,\\ S_{偶}=-160.\end{array}\right. $ 所以公比 $ q=\frac{S_{偶}}{S_{奇}}=\frac{-160}{-80}=2 $. 答案：2

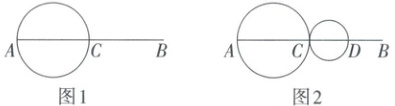
4. “一尺之棰,日取其半,万世不竭”出自《庄子·天下》,其中蕴含着数列的相关知识.已知长度为 $4$ 的线段 $AB$,取 $AB$ 的中点 $C$,以 $AC$ 为直径作圆(如图 1),该圆的面积为 $S_{1}$,在图 1 中取 $CB$ 的中点 $D$,以 $CD$ 为直径作圆(如图 2),图 2 中所有圆的面积之和为 $S_{2}$,以此类推,则 $S_{1}+S_{2}+… +S_{n}= $$\frac{4\pi}{9}\left[3n-1+\left(\frac{1}{4}\right)^{n}\right]$.

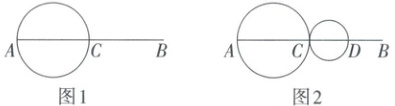
答案： 解析：由题意可知, 各圆的面积成以 $ \pi $ 为首项, $ \frac{1}{4} $ 为公比的等比数列, 故 $ S_{n}=\frac{\pi\left[1-\left(\frac{1}{4}\right)^{n}\right]}{1-\frac{1}{4}}=\frac{4\pi}{3}-\frac{4\pi}{3}×\left(\frac{1}{4}\right)^{n} $, 则 $ S_{1}+S_{2}+\cdots +S_{n}=\frac{4n\pi}{3}-\frac{\pi}{3}×\frac{1-\left(\frac{1}{4}\right)^{n}}{1-\frac{1}{4}}=\frac{4\pi}{9}\left[3n-1+\left(\frac{1}{4}\right)^{n}\right] $. 答案：$ \frac{4\pi}{9}\left[3n-1+\left(\frac{1}{4}\right)^{n}\right] $

1. 在等比数列$\{ a_{n}\}$中,$a_{1}= 4$,$a_{4}= 32$,则数列$\{ a_{n}\}$的前 10 项和为(D)
A.$2^{11}-2$
B.$2^{12}-2$
C.$2^{11}-4$
D.$2^{12}-4$

答案： 解析：选 D. 设等比数列$\{ a_{n}\} $的公比为 q,则$a_{4}=a_{1}q^{3}$,即 32= $4q^{3}$,解得$q=2$,则数列$\{ a_{n}\} $的前 10 项和为$\frac {a_{1}(1-q^{10})}{1-q}=$ $\frac {4×(1-2^{10})}{1-2}=2^{12}-4.$