《2025年黄冈小状元作业本六年级数学上册人教版重庆专版》

(1) 黑龙江肇东水库是最接近圆形的人工水库，直径大约是2km。这个水库的占地面积大约是(3.14)km²。

答案：
(1)3.14

(2) 云南真题 我国最早的统一货币是秦半两。如图所示的“半两钱”的外圆直径约32mm，内部正方形的边长约10mm，这枚“半两钱”正面的面积约是(703.84)mm²。

答案：
(2)703.84

(3) 在一个正方形里面画一个最大的圆，这个圆的周长是15.7cm，这个正方形的面积是(25)cm²。

答案：
(3)25

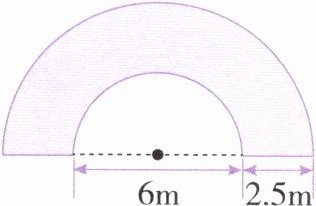
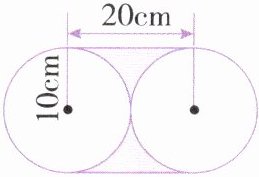
2. 计算下面左边图形的周长和右边图形涂色部分的面积。

答案：
2.左图:3.14×6÷2+3.14×(6÷2+2.5)+2.5×2=31.69(m)
解析:此题是求一个半圆环的周长。半圆环的周长=大圆周长的一半+小圆周长的一半+两个环宽。
右图:20×20−3.14×10²=86(cm²)
或0.86×10²=86(cm²)
解析:如图所示，分别延长两条半径。

涂色部分的面积=正方形的面积−一个圆的面积;也可以直接用公式0.86r²求出涂色部分的面积。

3. 一个底面是圆形的扫地机器人清扫一块地毯，这块地毯的两端是半圆形，中间是长方形。这块地毯的面积是多少平方分米？如果扫地机器人贴合着这块地毯边缘行进一周(如图)，扫地机器人圆形底面的半径是1.5dm，它的圆心走过路线的长度是多少分米？

答案： 3.面积:24×5×2+3.14×5²=318.5(dm²)
路线长度:24×2+2×3.14×(5+1.5)=88.82(dm)
解析:地毯的面积=长方形的面积+圆的面积;求圆心走过的路线的长度，其实就是求2条24dm的线段的长度和与一个半径为(5+1.5)dm的圆的周长之和。

4. 两块汉代玉璧，一块是外直径为18cm、内直径为8cm的圆环；另一块是外直径为16cm、内直径为8cm的圆环。这两块汉代玉璧的面积相差多少平方厘米？

答案： 4.方法1:3.14×(18÷2)²−3.14×(8÷2)²=204.1(cm²)
3.14×(16÷2)²−3.14×(8÷2)²=150.72(cm²)
204.1−150.72=53.38(cm²)
方法2:3.14×(18÷2)²−3.14×(16÷2)²=53.38(cm²)
解析:可以先分别求出两块玉璧的面积，再求出两块玉璧的面积差。也可以这样想:因为两块玉璧的内圆直径相等，所以两块玉璧的面积差就是大玉璧的外圆面积与小玉璧的外圆面积之差。

5. 观察并计算，你发现在外圆内方的图案中，圆与正方形的面积的比是(π:2)。(圆周率用π表示)

答案： 5.π:2
解析:可以通过计算得到结论。
第一幅图:
圆的面积:π×(2÷2)²=π(cm²)
正方形的面积:2×2÷2=2(cm²)
圆与正方形的面积的比:π:2
第二幅图:
圆的面积:π×(3÷2)²=2.25π(cm²)
正方形的面积:3×3÷2=4.5(cm²)
圆与正方形的面积的比:2.25π:4.5=π:2
第三幅图:
圆的面积:π×(4÷2)²=4π(cm²)
正方形的面积:4×4÷2=8(cm²)
圆与正方形的面积的比:4π:8=π:2