《2025年智慧学习明天出版社四年级数学上册人教版》

3. 一条路已经修了15天,每天修310米,还剩下1090米没修。这条路全长多少米?

答案： 310×15=4650(米)
4650+1090=5740(米)
答：这条路全长5740米。

4. 一辆客车和一辆货车同时从甲市开往乙市。客车每小时行78千米,货车每小时行65千米,4小时后两车相距多少千米?

答案： 解析：本题可根据两车的速度以及行驶时间，先求出两车的速度差，再根据路程 = 速度×时间，求出$4$小时后两车相距的距离；也可以分别求出两车$4$小时行驶的路程，再求它们的路程差。
方法一：先求速度差，再求路程差
步骤一：计算客车与货车的速度差
已知客车每小时行$78$千米，货车每小时行$65$千米，所以两车的速度差为：$78 - 65 = 13$（千米/小时）
步骤二：根据路程 = 速度×时间，计算$4$小时后两车相距的距离
两车行驶时间为$4$小时，速度差为$13$千米/小时，所以$4$小时后两车相距：$13×4 = 52$（千米）
方法二：分别求两车行驶路程，再求路程差
步骤一：根据路程 = 速度×时间，分别计算客车和货车$4$小时行驶的路程
客车每小时行$78$千米，行驶$4$小时，行驶的路程为：$78×4 = 312$（千米）
货车每小时行$65$千米，行驶$4$小时，行驶的路程为：$65×4 = 260$（千米）
步骤二：计算$4$小时后两车相距的距离
用客车行驶的路程减去货车行驶的路程，可得两车相距：$312 - 260 = 52$（千米）
答案：
方法一：
$(78 - 65)×4$
$= 13×4$
$= 52$（千米）
方法二：
$78×4 - 65×4$
$= 312 - 260$
$= 52$（千米）
答：$4$小时后两车相距$52$千米。

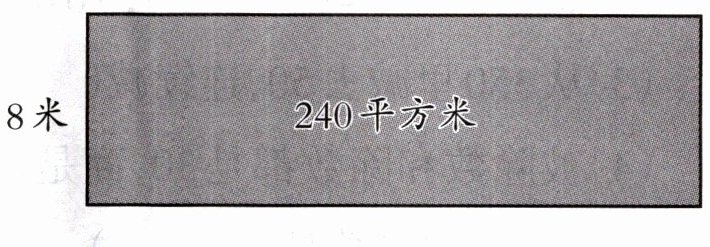
5. 下面是一块长方形绿地,如果长不变,宽增加到16米,增加后的绿地的面积是多少平方米?

答案： 解：
1. 首先根据长方形面积公式$S = a× b$（$S$表示面积，$a$表示长，$b$表示宽），已知原来宽$b_1 = 8$米，面积$S_1=240$平方米，求原来的长$a$：
由$a=\frac{S_1}{b_1}$，可得$a=\frac{240}{8}=30$米。
2. 然后求宽增加到$b_2 = 16$米时的面积$S_2$：
再根据$S = a× b$，此时$a = 30$米，$b = 16$米，所以$S_2=a× b_2$。
把$a = 30$，$b_2 = 16$代入公式，得$S_2=30×16 = 480$平方米。
答：增加后的绿地的面积是$480$平方米。

实验小学18位老师带领102名学生去参观科技馆。购票方案如下表所示,采用哪种方案买比较便宜?便宜多少钱?

答案： 解析：本题考查了方案选择问题。
要解决这个问题，需要先分别计算出两种方案所需的费用，然后进行比较。
方案一：
老师（成人）票费用：
$18 × 60 = 1080$（元），
学生票费用：
$102 × 30 = 3060$（元），
方案一总费用：
$1080 + 3060 = 4140$（元）。
方案二：
总人数：
$18 + 102 = 120$（人），
团体票费用：
$120 × 35 = 4200$（元）。
比较两种方案的费用：
$4140 \lt 4200$，
所以方案一更便宜。
便宜的金额：
$4200 - 4140 = 60$（元）。
答：采用方案一买比较便宜，便宜60元。