第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
(1)240×50的积的末尾有(
3
)个0。328×53的积是(五
)位数。
答案:
(1)计算240×50:先算24×5=120,因数末尾共有2个0,所以积为12000,末尾有3个0。
计算328×53:328×50=16400,328×3=984,16400+984=17384,17384是五位数。
3;五
(1)计算240×50:先算24×5=120,因数末尾共有2个0,所以积为12000,末尾有3个0。
计算328×53:328×50=16400,328×3=984,16400+984=17384,17384是五位数。
3;五
(2)单价×数量= (
总价
) 速度×时间= (路程
)
答案:
解析:题目考查的是单价、数量和总价之间的关系,以及速度、时间和路程之间的关系。这两个公式都是基础公式,需要直接记忆和应用。
答案:单价×数量=总价;速度×时间=路程。
答案:单价×数量=总价;速度×时间=路程。
(3)长方形草坪的面积是120平方米,将这个长方形草坪的长扩大到原来的3倍,宽不变,扩建后草坪的面积是(
360平方米
)。
答案:
解析:本题主要考察长方形面积的计算以及图形变换后面积的变化规律。
长方形的面积计算公式是$面积 = 长 × 宽$。
题目中说,长方形草坪的长扩大到原来的3倍,而宽保持不变。
设原来的长为L,宽为W,则原来的面积为$L × W = 120(平方米)$。
扩建后的长为3L,宽仍为W,所以扩建后的面积为:
$3L × W = 3 × (L × W) = 3 × 120 = 360(平方米)$。
答案:360平方米。
长方形的面积计算公式是$面积 = 长 × 宽$。
题目中说,长方形草坪的长扩大到原来的3倍,而宽保持不变。
设原来的长为L,宽为W,则原来的面积为$L × W = 120(平方米)$。
扩建后的长为3L,宽仍为W,所以扩建后的面积为:
$3L × W = 3 × (L × W) = 3 × 120 = 360(平方米)$。
答案:360平方米。
(4)65×34的积,乘(
10
)才能与650×34的积相等。
答案:
解析:
本题考查的是积的变化规律。
根据积的变化规律,一个因数不变,另一个因数扩大或缩小几倍(0除外),积也会随之扩大或缩小相同的倍数。
观察65×34与650×34,发现第一个乘数从65变成650,扩大了10倍,而第二个乘数34没有变化。
所以,为了保持积相等,需要将65×34的积也扩大10倍。
因此,65×34的积需要乘10才能与650×34的积相等。
答案:10。
本题考查的是积的变化规律。
根据积的变化规律,一个因数不变,另一个因数扩大或缩小几倍(0除外),积也会随之扩大或缩小相同的倍数。
观察65×34与650×34,发现第一个乘数从65变成650,扩大了10倍,而第二个乘数34没有变化。
所以,为了保持积相等,需要将65×34的积也扩大10倍。
因此,65×34的积需要乘10才能与650×34的积相等。
答案:10。
(1)下面的算式与740×19的结果相等的是(
①74×19 ②74×190 ③740×190
②
)。①74×19 ②74×190 ③740×190
答案:
解析:本题可根据积的变化规律来判断各个选项与$740×19$的结果是否相等。
积的变化规律为:在乘法算式中,一个因数扩大(或缩小)若干倍($0$除外),另一个因数缩小(或扩大)相同的倍数,积不变。
选项①:$740$变为$74$,$740÷74 = 10$,即$740$缩小了$10$倍,而$19$不变,根据积的变化规律,积会缩小$10$倍,所以$74×19$与$740×19$结果不相等。
选项②:$740$不变,$19$变为$190$,$190÷19 = 10$,即$19$扩大了$10$倍,一个因数不变,另一个因数扩大$10$倍,积也会扩大$10$倍;但也可以从另一个角度看,$740×19=(740÷10)×(19×10)=74×190$,积不变,所以$74×190$与$740×19$结果相等。
选项③:$740$不变,$19$变为$190$,积会扩大$10$倍,同时式子中$740$不变,整体积扩大了$10$倍,所以$740×190$与$740×19$结果不相等。
答案:②
积的变化规律为:在乘法算式中,一个因数扩大(或缩小)若干倍($0$除外),另一个因数缩小(或扩大)相同的倍数,积不变。
选项①:$740$变为$74$,$740÷74 = 10$,即$740$缩小了$10$倍,而$19$不变,根据积的变化规律,积会缩小$10$倍,所以$74×19$与$740×19$结果不相等。
选项②:$740$不变,$19$变为$190$,$190÷19 = 10$,即$19$扩大了$10$倍,一个因数不变,另一个因数扩大$10$倍,积也会扩大$10$倍;但也可以从另一个角度看,$740×19=(740÷10)×(19×10)=74×190$,积不变,所以$74×190$与$740×19$结果相等。
选项③:$740$不变,$19$变为$190$,积会扩大$10$倍,同时式子中$740$不变,整体积扩大了$10$倍,所以$740×190$与$740×19$结果不相等。
答案:②
(2)三位数乘两位数,积最少是(
①三位数 ②四位数 ③五位数
②
),最多是(③
)。①三位数 ②四位数 ③五位数
答案:
解析:本题考查三位数乘两位数积的位数情况。最小的三位数是$100$,最小的两位数是$10$,它们的积为$100×10 = 1000$,是四位数;最大的三位数是$999$,最大的两位数是$99$,它们的积为$999×99=999×(100 - 1)=99900 - 999 = 98901$,是五位数。所以三位数乘两位数,积最少是四位数,最多是五位数。
答案:②;③
答案:②;③
(3)一辆汽车每小时行驶80千米,6小时行驶多少千米? 这道题是求(
①速度 ②时间 ③路程
③
)。①速度 ②时间 ③路程
答案:
解析:题目描述了一辆汽车的速度和行驶时间,要求确定这是求什么的问题。根据题目描述,“每小时行驶80千米”是速度,“6小时”是时间,而题目问的是这两个条件下能求出什么。根据速度、时间和路程的关系,我们知道:路程 = 速度 × 时间。因此,这道题目实际上是要求出路程。
答案:③路程。
答案:③路程。
(4)小明的妈妈买了3千克樱桃,花了60元,每千克樱桃多少元? 解决这个问题时,用的数量关系是(
①单价×数量= 总价 ②数量×单价= 总价 ③总价÷数量= 单价
③
)。①单价×数量= 总价 ②数量×单价= 总价 ③总价÷数量= 单价
答案:
解析:本题考查单价、数量和总价之间的关系。
题目描述了小明的妈妈买了3千克樱桃,共花了60元,要求找出每千克樱桃的价格。
这里涉及的是单价、数量和总价之间的关系。
设每千克樱桃的价格为 x 元,则:
总价是 60 元,数量是 3 千克。
根据这些信息,可以建立以下关系:
总价 = 单价 × 数量
即:60 = x × 3
现在要解这个方程,找出 x 的值。
计算单价为:60÷3=20(元)。
用的数量关系是总价÷数量= 单价。
答案:③总价÷数量= 单价。
题目描述了小明的妈妈买了3千克樱桃,共花了60元,要求找出每千克樱桃的价格。
这里涉及的是单价、数量和总价之间的关系。
设每千克樱桃的价格为 x 元,则:
总价是 60 元,数量是 3 千克。
根据这些信息,可以建立以下关系:
总价 = 单价 × 数量
即:60 = x × 3
现在要解这个方程,找出 x 的值。
计算单价为:60÷3=20(元)。
用的数量关系是总价÷数量= 单价。
答案:③总价÷数量= 单价。
(5)下列算式中,与其他两个的积不同的是(
①200×86 ②2×860 ③860×20
②
)。①200×86 ②2×860 ③860×20
答案:
解析:本题考查的是整数的乘法运算。
分别计算三个算式的积:
①200×86=17200;
②2×860=1720;
③860×20=17200。
对比三个算式的积,可以发现:
算式①和算式③的积是相同的,都是17200,
而算式②的积是1720,与其他两个不同。
所以,与其他两个的积不同的是算式②。
答案:②。
分别计算三个算式的积:
①200×86=17200;
②2×860=1720;
③860×20=17200。
对比三个算式的积,可以发现:
算式①和算式③的积是相同的,都是17200,
而算式②的积是1720,与其他两个不同。
所以,与其他两个的积不同的是算式②。
答案:②。
(6)一个算式中,两个因数都乘2,积(
①也乘2 ②不变 ③乘4
③
)。①也乘2 ②不变 ③乘4
答案:
解析:
本题考查的是乘法运算中因数的变化对积的影响。
假设原来的两个因数是a和b,那么原来的积就是a×b。
现在,两个因数都乘以了2,所以新的因数是2a和2b。
新的积就是2a×2b=4a×b=4×(a×b),即原来的积乘以4。
答案:
③乘4。
本题考查的是乘法运算中因数的变化对积的影响。
假设原来的两个因数是a和b,那么原来的积就是a×b。
现在,两个因数都乘以了2,所以新的因数是2a和2b。
新的积就是2a×2b=4a×b=4×(a×b),即原来的积乘以4。
答案:
③乘4。
(7)每年3月12日为植树节,某年的主题是“共同呵护地球家园,筑造美丽未来”。为引导全社会积极行动,共同保护地球家园,四年级一班有31人参加了义务宣传活动,平均每人发放105份宣传单,他们一共发放了多少份宣传单? 乐乐用下面的竖式进行计算,竖式中箭头所指的部分表示(
①3人一共发放315份宣传单 ②31人一共发放3150份宣传单 ③30人一共发放315份宣传单 ④30人一共发放3150份宣传单
```
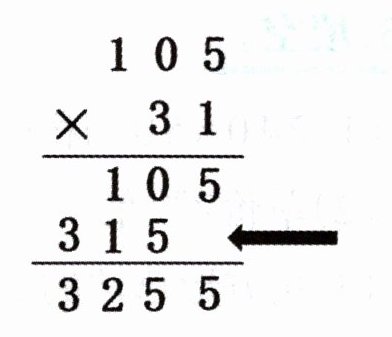
105
× 31
-----
105
315 ←———
-----
3255
```
④
)。①3人一共发放315份宣传单 ②31人一共发放3150份宣传单 ③30人一共发放315份宣传单 ④30人一共发放3150份宣传单
```
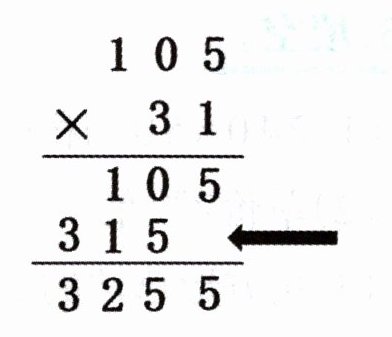
105
× 31
-----
105
315 ←———
-----
3255
```
答案:
解析:本题可根据乘法竖式的计算原理来分析箭头所指部分的意义。
在乘法竖式$105×31$中,先将$31$拆分为$30 + 1$,然后用$1$去乘$105$,得到$105$,再用$30$去乘$105$,得到$3150$(这里的$315$实际表示$3150$,因为$3$在十位上,代表$30$,$30×105 = 3150$ ),最后将这两个结果相加,即$105+3150 = 3255$。
所以箭头所指的$315$实际是$3150$,它表示$30$人一共发放$3150$份宣传单。
答案:④。
在乘法竖式$105×31$中,先将$31$拆分为$30 + 1$,然后用$1$去乘$105$,得到$105$,再用$30$去乘$105$,得到$3150$(这里的$315$实际表示$3150$,因为$3$在十位上,代表$30$,$30×105 = 3150$ ),最后将这两个结果相加,即$105+3150 = 3255$。
所以箭头所指的$315$实际是$3150$,它表示$30$人一共发放$3150$份宣传单。
答案:④。
查看更多完整答案,请扫码查看


