《2025年智慧学习明天出版社四年级数学上册人教版》

7. 一个长方形黑板的面积是9平方米,将这个黑板的长扩大到原来的3倍,宽不变,扩大后的面积是(27)平方米。

答案： 解析：
本题考查长方形面积的计算。
首先，我们需要知道长方形面积的计算公式，即面积 = 长 × 宽。
题目中给出原始的长方形黑板面积为9平方米。然后，题目描述了一个变化：黑板的长扩大到原来的3倍，而宽保持不变。
设原始长方形的长为l，宽为w，则原始面积 A = l × w = 9（平方米）。
变化后的长方形长为3l，宽仍为w，所以新的面积$ A' = 3l × w = 3 × (l × w) = 3 × 9 = 27$（平方米）。
所以，扩大后的长方形面积是27平方米。
答案：
27。

8. 在○里填上“＞”“＜”或“＝”。
985700○＜4370000
140×20○＝14×200
4768330○＞4763380
18×400○＞30×170

答案： 解析：本题考查了整数大小比较的方法，以及积不变的规律。
首先比较985700和4370000：
观察这两个数，985700是六位数，而4370000是七位数。
根据整数大小比较的方法，位数多的整数大于位数少的整数。
所以，985700 ＜ 4370000。
接着比较140 × 20和14 × 200：
根据积不变的规律，一个因数扩大（或缩小）若干倍（0除外），另一个因数缩小（或扩大）相同的倍数，积不变。
140是14的10倍，而200是20的10倍。
所以，140 × 20 = 14 × 200。
然后比较4768330和4763380：
这两个数都是七位数，且前三位数字都相同。
但第四位数字，一个是8，另一个是3，8大于3。
所以，4768330 ＞ 4763380。
最后比较18 × 400和30 × 170：
先计算两个乘积，18 × 400 = 7200，30 × 170 = 5100。
7200大于5100。
所以，18 × 400 ＞ 30 × 170。
答案：＜；＝；＞；＞。

9. 算盘上一颗上珠表示(5),一颗下珠表示(1)。

答案： 解析：算盘是中国传统的计算工具，在算盘上，每一档都有上珠和下珠，上珠表示$5$，下珠每个表示$1$。
答案：算盘上一颗上珠表示$5$，一颗下珠表示$1$。

10. 钟面上(6)时整,时针和分针的夹角是平角；(3)时整或(9)时整,时针与分针的夹角是直角。

答案： 解析：
本题考查钟面的认识，以及平角和直角的概念。
首先，要知道钟面上时针和分针是如何移动的。
在一个小时内，分针会走完整个钟面一圈，也就是360度；
而时针则只走1/12圈，也就是30度（因为360度/12小时 = 30度/小时）。
接下来，找出时针和分针夹角是平角（180度）的时间。
只有在6点整的时候，时针指向6，分针指向12，它们之间的夹角正好是180度，也就是平角。
然后，找出时针和分针夹角是直角（90度）的时间。
在3点整的时候，时针指向3，分针指向12，它们之间的夹角是90度，是直角。
在9点整的时候，时针指向9，分针指向12，它们之间的夹角也是90度，同样是直角。
答案：
钟面上
(6)时整，时针和分针的夹角是平角；
(3)时整或
(9)时整，时针与分针的夹角是直角。

11. 109□0000000≈109亿,□里最大填(4)。

答案： 解析：本题可根据“四舍五入”法求近似数的规则来确定$□$里可以填的数，进而得出最大能填的数。
“四舍五入”法是指在取小数近似数的时候，如果尾数的最高位数字是$4$或者比$4$小，就把尾数去掉；如果尾数的最高位数是$5$或者比$5$大，就把尾数舍去并且在它的前一位进“$1$”。
已知$109□0000000\approx109$亿，显然是用“四舍”法得到的近似数，所以$□$里可以填$1$、$2$、$3$、$4$，在这些数中最大的数是$4$。
答案：$4$。

12. 一列快车2小时行驶了320千米,它的平均速度是(160千米/小时)。

答案： 解析：本题可根据速度的计算公式来求解快车的平均速度，考查了速度、路程和时间三者之间的关系。
速度的计算公式为：速度 = 路程÷时间。
已知快车$2$小时行驶了$320$千米，其中路程是$320$千米，时间是$2$小时，将其代入公式可得平均速度为$320÷2 = 160$（千米/小时）。
答案：$160$千米/小时。

13. 一个长方形广场,长1250米,宽800米,它的面积是(1000000)平方米,合(100)公顷。

答案： 解析：本题主要考查长方形面积的计算以及面积单位的换算。首先，根据长方形面积的计算公式：面积 = 长 × 宽，可以计算出广场的面积。然后，需要将面积从平方米转换为公顷，根据$1公顷 = 10000平方米$进行单位换算。
长方形的面积计算公式为：
$面积 = 长 × 宽$
$= 1250 × 800$
$= 1000000 (平方米)$
根据$1公顷 = 10000平方米$，
所以$1000000 平方米 =1000000 ÷ 10000 = 100(公顷)$。
答案：$1000000$；$100$。

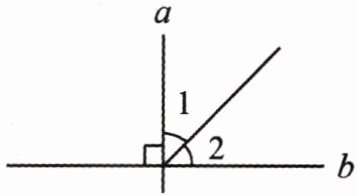
14. 右图中,∠1= ∠2,∠1= (45)°；直线a和直线b的位置关系是互相(垂直)。

答案： 解析：本题主要考查垂直的定义以及角度的计算。从图中可以看出$\angle1+\angle2 = 90^{\circ}$，又因为$\angle1=\angle2$，所以$\angle1$的度数为$90^{\circ}÷2 = 45^{\circ}$。根据垂直的定义：如果两条直线相交成直角，就说这两条直线互相垂直，由于$\angle1$和$\angle2$组成的角是直角，所以直线$a$和直线$b$互相垂直。
答案：$45$；垂直

15. 用5个6和4个0组成一个九位数,一个零也不读,这个数是(666660000)；读四个零,这个数是(606060606)。

答案： 解析：本题主要考查整数的读法，特别是零的读法规则。
整数的读法是从高位到低位，一级一级地读，每一级末尾的0都不读出来，其余数位连续几个0都只读一个零。
要想一个零也不读，就要把所有的零都写在每级的末尾。
要想读出四个零，就要把这$4$个零不能写在每级的末尾，且不能相邻。
答案：用$5$个$6$和$4$个$0$组成一个九位数，一个零也不读，这个数是$666660000$（答案不唯一，只要零都在最后即可）；
读四个零，这个数是$606060606$。

二、判断。(对的打“√”,错的打“×”)(每题1分,共5分)
1. 三位数乘两位数的积一定是四位数。(×)
2. 一个数的近似数不一定比这个数小。(√)
3. 与“万”相邻的两个计数单位分别是“千”和“十万”。(√)
4. 两个锐角的和一定比直角大。(×)
5. 从6时到12时,时针转了180°。(√)

答案： 解析：
1. 三位数乘两位数的积可能是四位数，也可能是五位数，还可能是六位数（如$100×10=1000$，$999×99=98901$，$500×200=100000$），因此该题说法错误。
2. 一个数的近似数是根据四舍五入等方法得到的，它可能比这个数大（如$56$近似为$60$），也可能比这个数小（如$54$近似为$50$），因此该题说法正确。
3. 在数位顺序表中，与“万”相邻的两个计数单位确实是“千”和“十万”，因此该题说法正确。
4. 两个锐角的和不一定比直角大，例如$30^\circ+30^\circ=60^\circ$，小于$90^\circ$，因此该题说法错误。
5. 从$6$时到$12$时，时针确实转了$180^\circ$，因为一圈是$360^\circ$，$6$小时占了一半，即$180^\circ$，因此该题说法正确。
答案：
1. ×
2. √
3. √
4. ×
5. √