《2025年名师面对面学科素养评价九年级数学全一册浙教版》

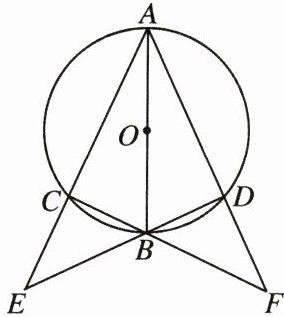
17. 如图,$AB$是$\odot O$的直径,$B$是$\overset{\frown}{CD}$的中点,弦$AC,DB$的延长线交于点$E$,弦$AD,CB$的延长线交于点$F$.
(1) 求证:$BE = BF$.
(2) 若$BD = 3$,$CE = 4$,求$\odot O$的直径.

答案：
17.
(1)证明:
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∵B是$\overset{\frown}{CD}$的中点,
∴$\overset{\frown}{BC}=\overset{\frown}{BD}$,
∴BC=BD,
∴△BCE≌△BDF(ASA),
∴BE=BF.
(2)解:
∵BC=BD=3,又
∵∠E=∠F,CE=4,
∴BE=$\sqrt{BC²+CE²}$=5,易证△ACB≌△ADB,
∴AC=AD.
设AC=AD=x,在Rt△ADE中,x²+8²=(x + 4)²,
解得x=6,即AC=6.
在Rt△ACB中,AB=$\sqrt{3²+6²}$=3$\sqrt{5}$,
即⊙O的直径为3$\sqrt{5}$.

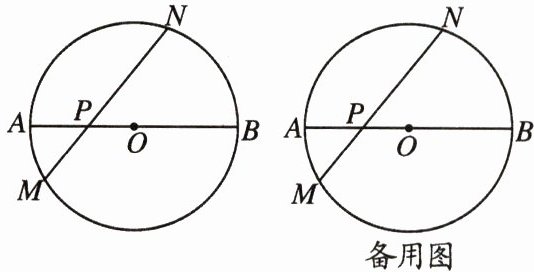
18. 如图,在$\odot O$中,$AB$是直径,$P$为$AB$上一点,过点$P$作弦$MN$,$\angle NPB = 45^{\circ}$.
(1) 若$AP = 2$,$BP = 6$,求$MN$的长.
(2) 若$MP = 3$,$NP = 5$,求$AB$的长.
(3) 当$P$在$AB$上运动时($\angle NPB = 45^{\circ}$不变),$\dfrac{PM^{2} + PN^{2}}{AB^{2}}$的值是否发生变化？若不变,请求出其值;若变化,请求出其范围.
 

答案：
18.解:
(1)作OH⊥MN于H,连结ON,
可求得MN=2NH=2$\sqrt{14}$.
(2)作OH⊥MN于H,连结ON,可求得
AB=2ON=2$\sqrt{17}$.
(3)$\frac{PM²+PN²}{AB²}$的值不发生变化,为定值$\frac{1}{2}$,作OH⊥MN于H,连结ON,则HM=HN,
设圆的半径为R,
在Rt△OHN中,OH²+NH²=ON²=R²,
在Rt△POH中,
∵∠OPH=45°,
∴OH=PH,
∴PH²+NH²=R²,
∵PM²+PN²=(HM - PH)²+(NH + PH)²=(NH - PH)²+(NH + PH)²=2(PH²+NH²)=2R².
又AB²=4R²,
∴$\frac{PM²+PN²}{AB²}$=$\frac{2R²}{4R²}$=$\frac{1}{2}$,
∴$\frac{PM²+PN²}{AB²}$的值不发生变化,为定值$\frac{1}{2}$.