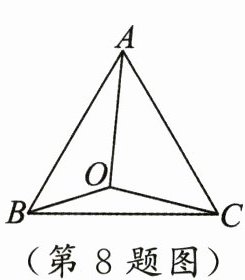
8. 如图,点$O$是等边三角形$ABC$内一点,$OA = 2,OB = 1,OC = \sqrt{3}$,则$\triangle AOB$与$\triangle BOC$的面积之和为 (
A.$\frac{\sqrt{3}}{4}$
B.$\frac{\sqrt{3}}{2}$
C.$\frac{3\sqrt{3}}{4}$
D.$\sqrt{3}$
C
)
A.$\frac{\sqrt{3}}{4}$
B.$\frac{\sqrt{3}}{2}$
C.$\frac{3\sqrt{3}}{4}$
D.$\sqrt{3}$
答案:
8.C
[解析]将△AOB绕点B顺时针旋转60°得△BCD,连结OD,
∴OB=OD,∠BOD=60°,CD=OA=2,
∴△BOD是等边三角形,
∴OD=OB=1,
∵$OD^{2}+OC^{2}=1^{2}+(\sqrt{3})^{2}=4$,$CD^{2}=2^{2}=4$,
∴$OD^{2}+OC^{2}=CD^{2}$,
∴∠DOC=90°,
∴△AOB与△BOC的面积之和为$S_{\triangle BOC}+S_{\triangle BCD}=S_{\triangle BOD}+S_{\triangle COD}=\frac{\sqrt{3}}{4}×1^{2}+\frac{1}{2}×1×\sqrt{3}=\frac{3\sqrt{3}}{4}$.

8.C
[解析]将△AOB绕点B顺时针旋转60°得△BCD,连结OD,
∴OB=OD,∠BOD=60°,CD=OA=2,
∴△BOD是等边三角形,
∴OD=OB=1,
∵$OD^{2}+OC^{2}=1^{2}+(\sqrt{3})^{2}=4$,$CD^{2}=2^{2}=4$,
∴$OD^{2}+OC^{2}=CD^{2}$,
∴∠DOC=90°,
∴△AOB与△BOC的面积之和为$S_{\triangle BOC}+S_{\triangle BCD}=S_{\triangle BOD}+S_{\triangle COD}=\frac{\sqrt{3}}{4}×1^{2}+\frac{1}{2}×1×\sqrt{3}=\frac{3\sqrt{3}}{4}$.

9. 在平面直角坐标系中,以点$O$为圆心、5为半径的$\odot O$与点$P(-4,4)$的位置关系是:点$P$在$\odot O$
外
(填“内”“上”或“外”).
答案:
9.外
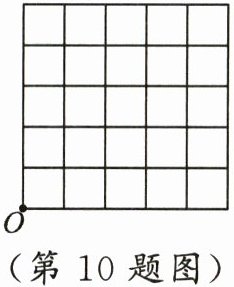
10. 如图,在$5×5$的正方形网格中,两条网格线的交点叫做格点,每个小正方形的边长均为1.以点$O$为圆心,5为半径画圆,共经过图中
4
个格点(包括图中网格边界上的点).
答案:
10.4
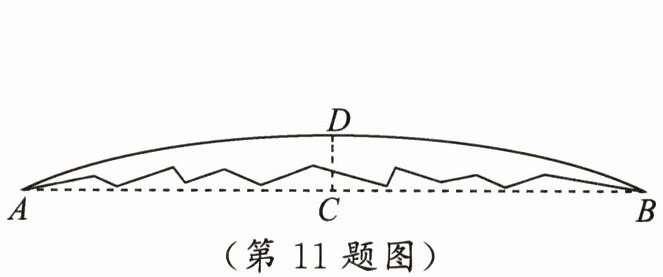
11. 一块圆形玻璃镜面碎成了几块,其中一块如图所示,测得弦$AB$长20厘米,弓形高$CD$为2厘米,则镜面半径为
26
厘米.
答案:
11.26
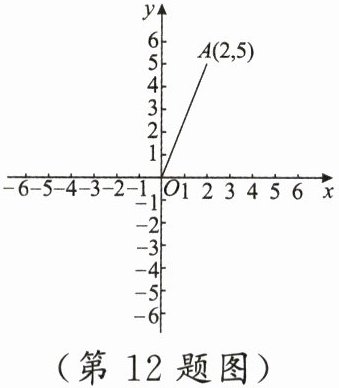
12. 如图,线段$OA$在平面直角坐标系内,点$A$的坐标为$(2,5)$,线段$OA$绕原点$O$逆时针旋转$90^{\circ}$,得到线段$OA'$,则点$A'$的坐标为
(−5,2)
.
答案:
12.(−5,2)
13. 如图,$AB$为$\odot O$的直径,点$D$是弧$AC$的中点,过点$D$作$DE\perp AB$于点$E$,延长$DE$交$\odot O$于点$F$.若$AC = 12,AE = 3$,则$\odot O$的直径长为
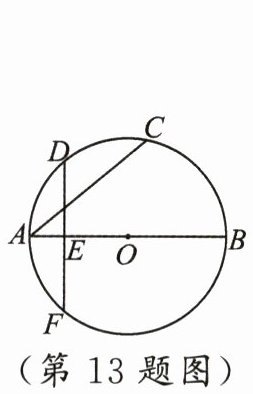
15
.
答案:
13.15 [解析]连结OF,首先证明AC=DF,在Rt△OEF中,利用勾股定理求解.
14. 如图,在正方形$ABCD$中,点$E$在边$DC$上,$DE = 5,EC = 3$,把线段$AE$绕点$A$旋转后使点$E$落在直线$BC$上的点$F$处,则$F,C$两点的距离为
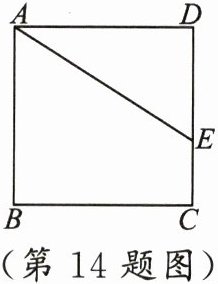
3或13
.
答案:
14.3或13 [解析]分点F在线段BC上和在射线CB上两种情况讨论.
查看更多完整答案,请扫码查看


