《2025年精彩练习就练这一本七年级数学上册浙教版评议教辅》

1. 若一个锐角α的补角是150°,则锐角α的度数是( )

A.30°
B.40°
C.130°
D.140°

答案： A

2. 下列图形中,∠1和∠2互为余角的是( )

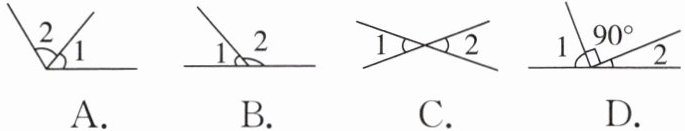
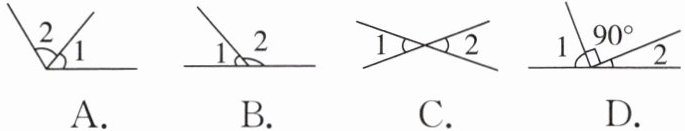
答案： D

3. 将一副直角三角尺按下图方式放置,若∠AOD= 22°,则∠BOC的大小为( )
]

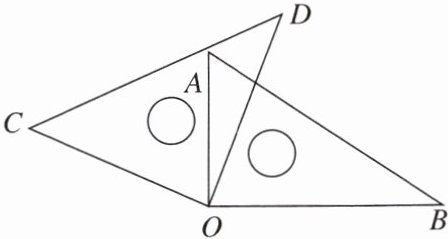
答案： D

4. 如图,点A在点O的北偏东60°的方向上,点B在点O的南偏东40°的方向上,则∠AOB的度数为( )
]

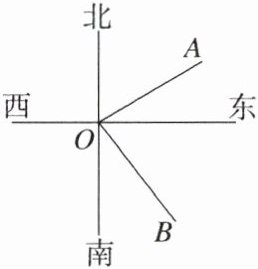
答案： B

5. 关于补角有下列四个叙述：①锐角的补角是钝角。②只有锐角才有补角。③互为补角的两个角不可能相等。④同角或等角的补角一定相等。其中正确的有( )

A.1个
B.2个
C.3个
D.4个

答案： B【解析】①若∠A 是锐角，则 180°-∠A＞90°，即锐角的补角是钝角，所以①正确。②任意角均有补角，所以②错误。③直角的补角是直角，所以互为补角的两个角也可能相等，故③错误。④同角或等角的补角相等，所以④正确。综上，正确的有①④，共 2 个。

6. 因为∠1+∠2= 90°,∠2+∠3= 90°,所以∠1= ∠3,根据是______。

答案： 同角的余角相等

7. 如图,将直角三角板的直角顶点放在直线l的点A处。若∠1= 28°18′,则∠2的度数是______。

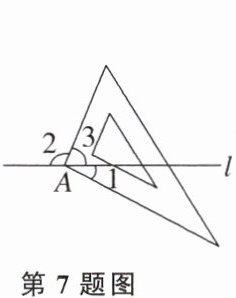
答案： 118°18′

8. 如图,若∠1和∠2都是∠α的余角,则∠1= ∠2。请说明理由(在括号内填上依据)。
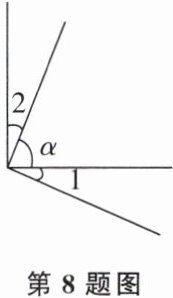
理由：因为∠1是∠α的余角(已知),所以∠1+∠α= 90°(余角的定义),所以∠1= 90°-∠α(等式的性质1)。因为∠2是∠α的余角(已知),所以∠2+∠α= 90°(______),所以∠2= 90°-∠α(______),所以∠1= ∠2(______)。

答案： 余角的定义 等式的性质 1 等量代换

9. 已知一个角的余角比这个角的补角的$\frac{1}{2}$小12°,求这个角和它的余角的度数。

答案： 解：设这个角的度数为α，由题意得 90°-α= $\frac{1}{2}$(180°-α)-12°，解得α=24°，它的余角的度数为 90°-α=90°-24°=66°，即这个角和它的余角的度数分别为 24°，66°。