【例 1】如图,E 是线段 AB 的中点,C 是 EB 上一点,且 EC:CB= 1:3,AC= 10 cm,求 AB 的长。
———A———E—C———B
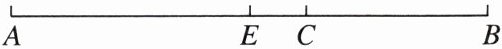
———A———E—C———B
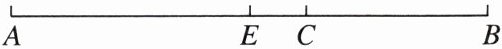
答案:
解:设EC的长为x cm,
因为EC:CB=1:3,
所以BC=3x,
所以BE=BC+CE=4x。
又因为E为线段AB的中点,
所以AE=BE=$\frac{1}{2}AB$,
所以AE=4x,AB=8x。
又因为AC=AE+EC,AC=10 cm,
所以5x=10,解得x=2,
所以AB=8x=16 cm。
因为EC:CB=1:3,
所以BC=3x,
所以BE=BC+CE=4x。
又因为E为线段AB的中点,
所以AE=BE=$\frac{1}{2}AB$,
所以AE=4x,AB=8x。
又因为AC=AE+EC,AC=10 cm,
所以5x=10,解得x=2,
所以AB=8x=16 cm。
【变式 1】如图,数轴上依次有 A,B,C 三点,它们对应的数分别是 a,b,c,若 BC= 2AB= 6,$a+b+c= 0$,则点 C 对应的数为 ( )
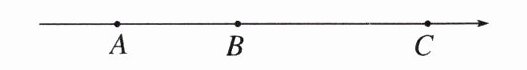
A.4
B.5
C.6
D.8
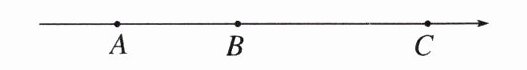
A.4
B.5
C.6
D.8
答案:
B 【解析】因为BC=2AB=6,
所以AB=3。
设点C表示的数为x,
所以点B表示x-6,点A表示x-9。
因为a+b+c=0,
所以x-9+x-6+x=0,
解得x=5。
所以AB=3。
设点C表示的数为x,
所以点B表示x-6,点A表示x-9。
因为a+b+c=0,
所以x-9+x-6+x=0,
解得x=5。
【变式 2】如图,点 B,C 在线段 AD 上,且 AB:BC:CD= 2:3:4,M 是线段 AC 的中点,N 是线段 CD 的中点,且 MN= 9。求 BD 的长。
A——B M——C——N——D
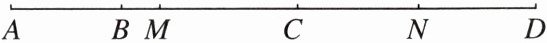
A——B M——C——N——D
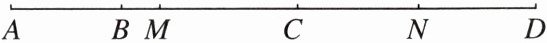
答案:
解:设AB=2x,
因为AB:BC:CD=2:3:4,
所以BC=3x,CD=4x。
因为M是线段AC的中点,N是线段CD的中点,
所以CM=$\frac{1}{2}AC$,CN=$\frac{1}{2}CD$,
所以MN=CM+CN=$\frac{1}{2}(AC+CD)$=$\frac{1}{2}AD$=9,
所以AD=18,
所以BD=$\frac{3+4}{2+3+4}× AD$=14。
因为AB:BC:CD=2:3:4,
所以BC=3x,CD=4x。
因为M是线段AC的中点,N是线段CD的中点,
所以CM=$\frac{1}{2}AC$,CN=$\frac{1}{2}CD$,
所以MN=CM+CN=$\frac{1}{2}(AC+CD)$=$\frac{1}{2}AD$=9,
所以AD=18,
所以BD=$\frac{3+4}{2+3+4}× AD$=14。
【例 2】如图,已知 AB= 24,C 是线段 AB 的中点。若点 D 在线段 AB 上,且满足 BD= 3CD。你认为有几种可能?根据题意在图中标出点 D 的大致位置,求 CD 的长。
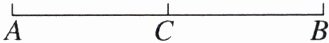
———A———C———B
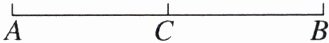
———A———C———B
答案:
解:有两种情况:
①当点D在点C左侧时,如图1。
因为AB=24,C是线段AB的中点,
所以BC=$\frac{1}{2}AB$=12。
因为BD=3CD,
所以BC=2CD,
所以2CD=12,
解得CD=6;
②当点D在点C右侧时,如图2。
因为AB=24,C是线段AB的中点,
所以BC=$\frac{1}{2}AB$=12。
因为BD=3CD,
所以BC=4CD,
所以4CD=12,
解得CD=3。
综上所述,CD的长为6或3。
①当点D在点C左侧时,如图1。
因为AB=24,C是线段AB的中点,
所以BC=$\frac{1}{2}AB$=12。
因为BD=3CD,
所以BC=2CD,
所以2CD=12,
解得CD=6;
②当点D在点C右侧时,如图2。
因为AB=24,C是线段AB的中点,
所以BC=$\frac{1}{2}AB$=12。
因为BD=3CD,
所以BC=4CD,
所以4CD=12,
解得CD=3。
综上所述,CD的长为6或3。
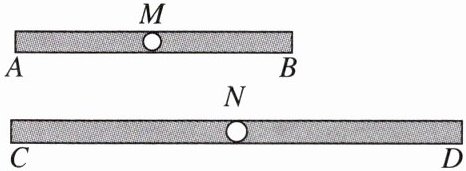
【变式】有两根木条 AB 和 CD,AB 的长为 80 cm,CD 的长为 130 cm,在它们的中点处各有一个小圆孔 M,N(圆孔直径忽略不计,M,N 抽象成两个点),将它们的一端重合,放置在同一条直线上,此时两根木条的小圆孔之间的距离 MN= ( )
A.25 cm
B.105 cm
C.25 cm 或 105 cm
D.50 cm 或 210 cm

A.25 cm
B.105 cm
C.25 cm 或 105 cm
D.50 cm 或 210 cm
答案:
C 【解析】当点A,C(或点B,D)重合,且剩余两端点在重合点同侧时,如图1,
MN=CN-AM=$\frac{1}{2}CD-\frac{1}{2}AB$
=65-40=25(cm)。
当点B,C(或点A,D)重合,且剩余两端点在重合点两侧时,如图2,
MN=CN+BM=$\frac{1}{2}CD+\frac{1}{2}AB$
=65+40=105(cm)。
综上所述,两根木条的小圆孔之间的距离MN=25 cm或105 cm。
MN=CN-AM=$\frac{1}{2}CD-\frac{1}{2}AB$
=65-40=25(cm)。
当点B,C(或点A,D)重合,且剩余两端点在重合点两侧时,如图2,
MN=CN+BM=$\frac{1}{2}CD+\frac{1}{2}AB$
=65+40=105(cm)。
综上所述,两根木条的小圆孔之间的距离MN=25 cm或105 cm。
查看更多完整答案,请扫码查看


