《2025年精彩练习就练这一本七年级数学上册浙教版评议教辅》

9. 计算：
(1)$26+14+(-16)$。
(2)$4.7+(-0.8)+5.3+(-8.2)$。
(3)$\frac{1}{2}+\left(-\frac{2}{3}\right)+\frac{4}{5}+\left(-\frac{1}{2}\right)+\left(-\frac{1}{3}\right)$。
(4)$43+(-77)+27+(-43)$。

答案： 解：
(1)原式=(26+14)+(-16)
=40+(-16)
=24。
(2)原式=(4.7+5.3)+[(-0.8)+(-8.2)]
=10+(-9)
=1。
(3)原式=$[\frac{1}{2}+(-\frac{1}{2})]+[(-\frac{2}{3})+(-\frac{1}{3})]+\frac{4}{5}$
=0+(-1)+$\frac{4}{5}$
=$-\frac{1}{5}$。
(4)原式=[43+(-43)]+[(-77)+27]
=0+(-50)=-50。

10. 如果$a+b+c= 0$,且$|a|＞|b|＞|c|$,那么下列式子可能成立的是 ( )

A.$c＞0$,$a＜0$
B.$b＜0$,$c＞0$
C.$b＞0$,$c＜0$
D.$b= 0$

答案： A

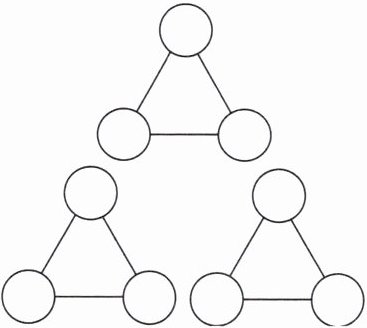
11. 下图是三个三角形,每个三角形的顶点处都有一个“○”,在每个“○”中填入一个数,满足这三个三角形的3个顶点处的“○”中的数的和都等于2。
(1)将$-8,-7,-6,-4,1,3,5,9,13$这9个数填入恰当的位置,使得这三个三角形的3个顶点处的“○”中的数的和都等于2。
(2)如果将(1)中的这9个数改为$-13,-9,-5,-3,-1,4,6,7,8$,还能满足要求吗？如果满足,请再画三个三角形并把数字填在“○”中；如果不满足,请说明理由。

答案：
解：
(1)如图所示。

(2)不能,理由如下：
因为(-13)+(-9)+(-5)+(-3)+(-1)+4+6+7+8=(-31)+25=-6,
所以如果将
(1)中的这9个数改为-13,-9,-5,-3,-1,4,6,7,8,不能满足要求。