《2025年天星教育28天预习新高一物理》

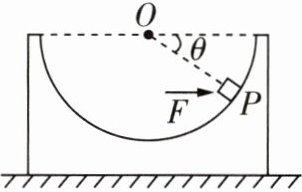
1.如图所示,光滑半球形容器固定在水平面上,O为球心。一质量为m的滑块,在水平力F的作用下静止于P点,设滑块所受支持力为$F_{N}$,OP与水平方向的夹角为$\theta$。重力加速度为g,下列关系式正确的是
( )

A.$F= \frac{mg}{\tan\theta}$
B.$F= mg\tan\theta$
C.$F_{N}= \frac{mg}{\tan\theta}$
D.$F_{N}= mg\tan\theta$

答案：
对滑块进行受力分析，如图所示，将$F_{N}$沿水平方向和竖直方向进行正交分解，根据平衡条件列方程，水平方向有$F_{x}=F_{N}\cos \theta =F$，竖直方向有$F_{y}=F_{N}\sin \theta =mg$，联立解得$F_{N}=\frac{mg}{\sin \theta}$，$F=\frac{mg}{\tan \theta}$，故A正确。

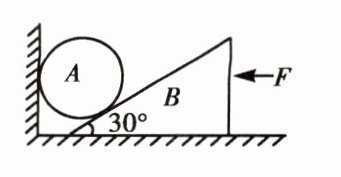
典例2 如图所示,A球重$G_{1}= 60N$,斜面体B重$G_{2}= 100N$,斜面倾角为$30^{\circ}$,一切摩擦均不计。则水平力F为多大时,才能使A、B均处于静止状态？求此时竖直墙壁和水平面受到的压力大小。

答案： 解：
解法一（隔离法）
1. 对球A受力分析（重力$G_1$、墙壁支持力$F_1$、斜面支持力$F_2$）：
由平衡条件：
$F_2\sin30^\circ = F_1$，
$F_2\cos30^\circ = G_1$。
代入$G_1=60\,\text{N}$，解得：
$F_2=\frac{G_1}{\cos30^\circ}=\frac{60}{\frac{\sqrt{3}}{2}}=40\sqrt{3}\,\text{N}$，
$F_1=G_1\tan30^\circ=60×\frac{\sqrt{3}}{3}=20\sqrt{3}\,\text{N}$。
2. 对斜面体B受力分析（重力$G_2$、水平力$F$、地面支持力$F_3$、A的压力$F_2'$，$F_2'=F_2$）：
由平衡条件：
$F=F_2'\sin30^\circ$，
$F_3=G_2+F_2'\cos30^\circ$。
代入数据解得：
$F=40\sqrt{3}×\frac{1}{2}=20\sqrt{3}\,\text{N}$，
$F_3=100+40\sqrt{3}×\frac{\sqrt{3}}{2}=160\,\text{N}$。
解法二（整体法）
对A、B整体受力分析（总重力$G_1+G_2$、水平力$F$、墙壁支持力$F_1$、地面支持力$F_3$）：
由平衡条件：
水平方向：$F=F_1$，
竖直方向：$F_3=G_1+G_2=160\,\text{N}$。
结合隔离A的分析，得$F_1=20\sqrt{3}\,\text{N}$，故$F=20\sqrt{3}\,\text{N}$。
结论
水平力$F=20\sqrt{3}\,\text{N}$；竖直墙壁受到的压力为$20\sqrt{3}\,\text{N}$；水平面受到的压力为$160\,\text{N}$。
答案：$20\sqrt{3}\,\text{N}$；$20\sqrt{3}\,\text{N}$；$160\,\text{N}$