《2025年天星教育28天预习新高一物理》

3.(2025·湖南长沙雅礼中学月考)如图所示,某校物理兴趣小组为了了解高空坠物的危害,将一只鸡蛋从离地面$h = 20m$高的高楼面由静止释放,鸡蛋下落途中用$\Delta t = 0.2s$的时间通过一个窗口,窗口的高度为$\Delta h = 2m$,忽略空气阻力,重力加速度$g取10m/s^{2}$,求：
(1)鸡蛋从释放到落地所用的时间$t及落地前瞬间速度的大小v$；
(2)鸡蛋经过窗口上边沿瞬间的速度大小。

答案：
(1) $2s$ $20m/s$
(2) $9m/s$
(1) 根据自由落体运动位移与时间的关系有 $h=\frac{1}{2}gt^{2}$
解得 $t = 2s$
鸡蛋落地前瞬间的速度大小为 $v = gt = 20m/s$。
(2) 设鸡蛋经过窗口上沿瞬间的速度大小为 $v_{1}$，根据匀变速直线运动规律，有 $\Delta h = v_{1}\Delta t+\frac{1}{2}g(\Delta t)^{2}$
解得 $v_{1}=9m/s$。

4.新创新实验 某学习小组用如图所示装置测量当地的重力加速度。两光电门固定于铁架台上,光电门1、2与光电计时器相连,小球与光电门1、2在同一竖直线上。
(1)让小球紧靠固定挡板,由静止释放,光电计时器记录小球经过光电门1和光电门2所用的时间$t_{1}$、$t_{2}$,测出两光电门间的高度差$h$,小球直径为$d$,则小球经过光电门1的速度大小$v_{1}= $______,小球经过光电门2的速度大小$v_{2}= $______。(用测得的物理量符号表示)

(2)重力加速度$g = $______(用测得的$v_{1}$、$v_{2}$、$h$表示)。

答案：

(1) $\frac{d}{t_{1}}$ $\frac{d}{t_{2}}$
(2) $\frac{v_{2}^{2}-v_{1}^{2}}{2h}$
实验原理剖析：
(1) 利用光电门求瞬时速度→球穿过光电门的时间非常短→平均速度近似等于瞬时速度→$v=\frac{\Delta x}{\Delta t}$。
(2) 已知小球穿过两光电门时的瞬时速度和两光电门的距离→利用速度—位移公式 $v^{2}-v_{0}^{2}=2gh$ 求重力加速度。
实验装置分析：利用光电门求瞬时速度→小球穿过光电门的时间很短→平均速度代替小球通过光电门时的瞬时速度→$v_{1}=\frac{d}{t_{1}}$，$v_{2}=\frac{d}{t_{2}}$。已知两光电门间的高度差 $h$，瞬时速度 $v_{1}$、$v_{2}$→由速度—位移公式得 $2gh = v_{2}^{2}-v_{1}^{2}$→$g=\frac{v_{2}^{2}-v_{1}^{2}}{2h}$。

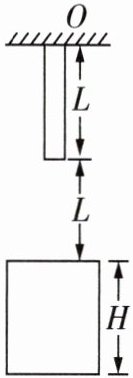
5.一根长为$L$的棒,上端悬挂在天花板上的$O$点,在棒的正下方,距棒的下端也为$L处固定着一个高为H$的圆筒,如图所示,棒被释放后做自由落体运动。求：(重力加速度为$g$)
(1)棒的下端到达圆筒上端时棒的速度大小$v$；
(2)棒通过圆筒所用的时间$t$。

答案：

(1) $\sqrt{2gL}$
(2) $\sqrt{\frac{4L + 2H}{g}}-\sqrt{\frac{2L}{g}}$
(1) 设棒下落 $L$ 时的速度为 $v$，由位移与速度的关系式解得 $v=\sqrt{2gL}$。
(2) 图解过程如图所示，棒刚刚进入圆筒时下落的距离为 $L$，棒刚刚穿过圆筒时下落的距离为 $h = 2L + H$
由位移与时间的关系式得 $L=\frac{1}{2}gt_{1}^{2}$
$h = 2L + H=\frac{1}{2}gt_{2}^{2}$
解得 $t_{1}=\sqrt{\frac{2L}{g}}$，$t_{2}=\sqrt{\frac{4L + 2H}{g}}$
所以棒通过圆筒所用的时间
$t = t_{2}-t_{1}=\sqrt{\frac{4L + 2H}{g}}-\sqrt{\frac{2L}{g}}$。