《2025年天星教育28天预习新高一物理》

典例2 如图所示为A、B两物体由同一地点沿相同的方向做直线运动的v-t图像,由图可知(   )


A.A运动后的加速度为$\frac {4}{3}m/s^{2}$
B.第10s末A、B相遇
C.第15s末A已运动到B的前方
D.A、B再次相遇前,它们之间的最大距离为75m

答案：

答案：D

1. 汽车以18m/s的速度在水平路面上匀速前进,紧急制动后做匀减速直线运动,加速度大小为$4m/s^{2}$,则刹车后5s时汽车的速度为(A)
A.0
B.2m/s
C.-2m/s
D.3m/s

答案： 1.A　汽车速度减为零的时间$t_{0}=\frac{v_{0}}{a}=\frac{18}{4}s=4.5s＜5s$，则
[敲黑板]利用逆向思维法，将正向的匀减速直线运动，逆向看成匀加速直线运动
刹车后5s时的速度为0，A正确。

2. 新生命现象 猎豹追捕猎物时运动的最大加速度可达$9m/s^{2}$,最大速度可达30m/s。羚羊被猎豹追捕时的最大加速度可达$12.5m/s^{2}$,最大速度可达25m/s,当猎豹潜伏点距羚羊20m时会被羚羊发现。设从此时开始两者同时由静止在同一直线上一追一逃,尽力奔跑,达到各自最大速度后开始匀速运动,则(B)
A.两动物加速运动的时间相等
B.在羚羊达到最大速度之前,两动物间的距离越来越大
C.在猎豹达到最大速度之前,两动物间的距离越来越小
D.猎豹速度达到最大速度30m/s时,两动物相距最远

答案： 2.B　猎豹和羚羊加速运动的时间分别为$t_{豹}=\frac{10}{3}s$，$t_{羊}=2s$，A错误；因为羚羊的最大加速度大，所以在羚羊达到最大速度之前，羚羊的速度一直大于猎豹的速度，二者之间的距离越来越大，B正确；因为羚羊的速度先达到最大，所以在猎豹达到最大速度之前，两动物间的距离先增大后减小，C错误；根据运动规律可知，当猎豹的速度与羚羊的最大速度相同，即达到25m/s时，两动物相距最远，之后猎豹的速度
[点关键]在分析追及相遇问题时，两物体速度相等是二者距离最近、距离最远或能否追上的临界条件
大于羚羊的速度，两动物间的距离会越来越小，D错误。

3. (2025·河北石家庄一中月考)两辆完全相同的汽车,沿水平直线一前一后匀速行驶,速度均为$v_{0}$,若前车突然以恒定加速度刹车,在它刚停车后,后车以与前车相同的加速度开始刹车,已知前车在刹车过程中所行驶的距离为x,若要保证两车在上述情况下不相撞,则两车在匀速行驶时至少应保持的距离为( )

A.x
B.2x
C.3x
D.4x

答案：
3.B　从前车刹车开始计时，作出两车的速度—时间图像如图所示。后车比前车多通过的位移等于图中所画阴影部分的面积，其值为前车位移$x=\frac{v_{0}t_{0}}{2}$的两倍，故为保证两车不相撞，至少应相隔$2x$。B正确。

4. 一辆长途客车正在以$v_{0}= 20m/s$的速度匀速行驶。突然,司机看见车的正前方34m处有一只狗,如图甲所示(以该时刻为$t= 0$时刻),长途客车的速度—时间图像如图乙所示,客车司机的反应时间为$Δt= 0.5s$。
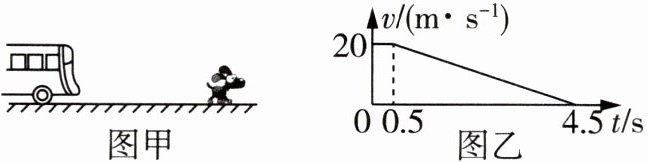
(1)求从司机发现狗至长途客车停止运动的这段时间内客车前进的距离；
(2)求长途客车制动时的加速度；
(3)若狗正以$v_{1}= 4m/s$的速度与长途客车同向奔跑,狗能否摆脱被撞的噩运？

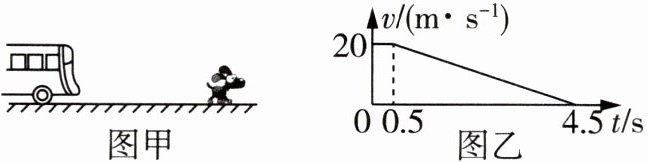
答案：
(1)50m　
(2)$5m/s^{2}$，方向与初速度方向相反　
(3)能摆脱被撞的噩运
(1)$v - t$图线与坐标轴围成的面积表示位移，可知从司机发现狗至长途客车停止运动的这段时间内，客车前进的距离$x = 20×0.5m+\frac{1}{2}×20×(4.5 - 0.5)m=50m$。
(2)长途客车制动时的加速度
$a=\frac{\Delta v}{\Delta t'}=\frac{0 - 20}{4.5 - 0.5}m/s^{2}=-5m/s^{2}$，方向与初速度方向相反。
(3)当客车速度减小到与狗的速度相等时，有$v_{0}+at = v_{1}$，解
[释疑惑]客车恰好不撞上狗的临界条件是二者速度相同时位移差等于34m，若位移差小于或等于34m，狗能够摆脱被撞的噩运。
得$t = 3.2s$
客车从刹车到与狗的速度相等这段时间行驶的距离
$x_{车}=v_{0}\Delta t+\frac{v_{0}+v_{1}}{2}t=48.4m$
狗奔跑的距离$x_{狗}=v_{1}(\Delta t + t)=14.8m$
因$x_{车}-x_{狗}=33.6m＜34m$，所以小狗能摆脱被撞的噩运。