2025年天星教育28天预习新高一物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年天星教育28天预习新高一物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
1. (多选)四只蚂蚁同时从圆形轨道的 $A$ 点出发,分别沿 $ABC$ 和 $ADE$ 方向爬行,经过相同的时间分别到达 $B$、$C$、$D$、$E$ 四个位置,以下说法正确的是( )

A. 爬到 $B$、$D$ 位置的两只蚂蚁,位移相同
B. 爬到 $B$、$D$ 位置的两只蚂蚁,路程可能相同
C. 爬到 $C$、$E$ 位置的两只蚂蚁,平均速度相同
D. 爬到 $C$、$E$ 位置的两只蚂蚁,平均速率可能相同

A. 爬到 $B$、$D$ 位置的两只蚂蚁,位移相同
B. 爬到 $B$、$D$ 位置的两只蚂蚁,路程可能相同
C. 爬到 $C$、$E$ 位置的两只蚂蚁,平均速度相同
D. 爬到 $C$、$E$ 位置的两只蚂蚁,平均速率可能相同
答案:
BD
爬到 B、D 位置的两只蚂蚁,位移方向不同,路程可能相同,A 错误,B 正确。
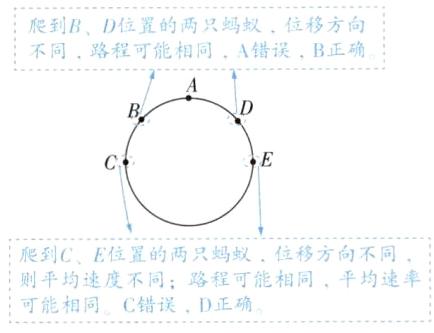
爬到 C、E 位置的两只蚂蚁,位移方向不同,则平均速度不同;路程可能相同,平均速率可能相同。C 错误,D 正确。
[避易错]题中未说明$\overset{\frown}{AB}=\overset{\frown}{AD}$,不能想当然认为爬到 B、D 位置的两只蚂蚁路程一定相同。
BD
爬到 B、D 位置的两只蚂蚁,位移方向不同,路程可能相同,A 错误,B 正确。

爬到 C、E 位置的两只蚂蚁,位移方向不同,则平均速度不同;路程可能相同,平均速率可能相同。C 错误,D 正确。
[避易错]题中未说明$\overset{\frown}{AB}=\overset{\frown}{AD}$,不能想当然认为爬到 B、D 位置的两只蚂蚁路程一定相同。
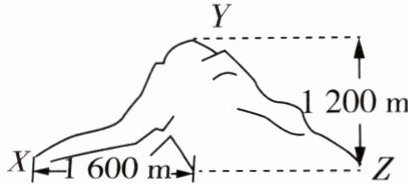
典例 2 登山运动员用时 $1h40min$ 由宿营地 $X$ 点爬到山顶 $Y$ 点,在山道上通过的路程是 $2400m$,相对于 $X$ 点升高了 $1200m$,如图所示。
(1)计算运动员由 $X$ 点到 $Y$ 点的位移。
(2)计算他爬山的平均速率。
(3)计算他爬山的平均速度的大小。
解析 (1)位移大小等于初、末位置间的距离,$X$ 点到 $Y$ 点的位移大小为 $x = \sqrt{1200^2 + 1600^2}m = 2000m$,方向由 $X$ 指向 $Y$。
(2)平均速率为 $\overline{v} = \frac{s}{t} = \frac{2400}{6000}m/s = 0.4m/s$。
【避易错】平均速率是路程与时间的比,是标量;平均速度是位移与时间的比,是矢量。
(3)平均速度大小为 $\overline{v'} = \frac{x}{t} = \frac{2000}{6000}m/s = 0.33m/s$。

(1)计算运动员由 $X$ 点到 $Y$ 点的位移。
(2)计算他爬山的平均速率。
(3)计算他爬山的平均速度的大小。
解析 (1)位移大小等于初、末位置间的距离,$X$ 点到 $Y$ 点的位移大小为 $x = \sqrt{1200^2 + 1600^2}m = 2000m$,方向由 $X$ 指向 $Y$。
(2)平均速率为 $\overline{v} = \frac{s}{t} = \frac{2400}{6000}m/s = 0.4m/s$。
【避易错】平均速率是路程与时间的比,是标量;平均速度是位移与时间的比,是矢量。
(3)平均速度大小为 $\overline{v'} = \frac{x}{t} = \frac{2000}{6000}m/s = 0.33m/s$。
答案:
【解析】:
本题主要考查位移、路程、平均速率和平均速度的计算。
(1)位移是初位置指向末位置的有向线段,从图中可看出运动员由$X$到$Y$的位移,其水平位移为$1600m$(通过山道水平距离和升高距离利用勾股定理计算得出水平距离为$\sqrt{2400^{2}-1200^{2}} = 1600m$ ),竖直位移为$1200m$,根据勾股定理可算出位移大小。
(2)平均速率是路程与时间的比值,已知路程为$2400m$,时间为$1h40min$,将其换算为秒后代入公式计算。
(3)平均速度是位移与时间的比值,已求得位移大小为$2000m$,时间同样为$1h40min$,换算为秒后代入公式计算。
(1)位移是初位置指向末位置的有向线段,从$X$到$Y$,水平位移$x_1 = 1600m$,竖直位移$x_2 = 1200m$,根据勾股定理,位移大小$x=\sqrt{1600^{2}+1200^{2}} = 2000m$,方向由$X$指向$Y$。
(2)已知通过的路程$s = 2400m$,时间$t = 1h40min=1×3600 + 40×60 = 6000s$,根据平均速率公式$\overline{v}=\frac{s}{t}$,可得$\overline{v}=\frac{2400}{6000}=0.4m/s$。
(3)位移$x = 2000m$,时间$t = 6000s$,根据平均速度公式$\overline{v}'=\frac{x}{t}$,可得$\overline{v}'=\frac{2000}{6000}\approx0.33m/s$。
【答案】:
(1)$2000m$,由$X$指向$Y$;
(2)$0.4m/s$;
(3)$0.33m/s$
本题主要考查位移、路程、平均速率和平均速度的计算。
(1)位移是初位置指向末位置的有向线段,从图中可看出运动员由$X$到$Y$的位移,其水平位移为$1600m$(通过山道水平距离和升高距离利用勾股定理计算得出水平距离为$\sqrt{2400^{2}-1200^{2}} = 1600m$ ),竖直位移为$1200m$,根据勾股定理可算出位移大小。
(2)平均速率是路程与时间的比值,已知路程为$2400m$,时间为$1h40min$,将其换算为秒后代入公式计算。
(3)平均速度是位移与时间的比值,已求得位移大小为$2000m$,时间同样为$1h40min$,换算为秒后代入公式计算。
(1)位移是初位置指向末位置的有向线段,从$X$到$Y$,水平位移$x_1 = 1600m$,竖直位移$x_2 = 1200m$,根据勾股定理,位移大小$x=\sqrt{1600^{2}+1200^{2}} = 2000m$,方向由$X$指向$Y$。
(2)已知通过的路程$s = 2400m$,时间$t = 1h40min=1×3600 + 40×60 = 6000s$,根据平均速率公式$\overline{v}=\frac{s}{t}$,可得$\overline{v}=\frac{2400}{6000}=0.4m/s$。
(3)位移$x = 2000m$,时间$t = 6000s$,根据平均速度公式$\overline{v}'=\frac{x}{t}$,可得$\overline{v}'=\frac{2000}{6000}\approx0.33m/s$。
【答案】:
(1)$2000m$,由$X$指向$Y$;
(2)$0.4m/s$;
(3)$0.33m/s$
2. 一质点从 $O$ 点出发,沿 $x$ 轴正方向做直线运动,它的位移大小与时间的关系式为 $x = 4t^2(m)$。
(1)求 $t_1 = 3s$ 到 $t_1' = 5s$ 这段时间内的平均速度大小;
(2)求 $t_1 = 3s$ 到 $t_2 = 3.1s$ 这段时间内的平均速度大小;
(3)求 $t_1 = 3s$ 到 $t_3 = 3.01s$ 这段时间内的平均速度大小;
(4)通过以上计算,你认为哪个平均速度大小更接近 $t_1 = 3s$ 时刻的瞬时速度大小?
(1)求 $t_1 = 3s$ 到 $t_1' = 5s$ 这段时间内的平均速度大小;
(2)求 $t_1 = 3s$ 到 $t_2 = 3.1s$ 这段时间内的平均速度大小;
(3)求 $t_1 = 3s$ 到 $t_3 = 3.01s$ 这段时间内的平均速度大小;
(4)通过以上计算,你认为哪个平均速度大小更接近 $t_1 = 3s$ 时刻的瞬时速度大小?
答案:
(1)32 m/s
(2)24.4 m/s
(3)24.04 m/s
(4)见解析
(1)$\overline{v}_{1}=\frac{\Delta x_{1}}{\Delta t_{1}}=\frac{4×(5^{2}-3^{2})}{5 - 3}m/s = 32m/s$。
(2)$\overline{v}_{2}=\frac{\Delta x_{2}}{\Delta t_{2}}=\frac{4×(3.1^{2}-3^{2})}{3.1 - 3}m/s = 24.4m/s$。
(3)$\overline{v}_{3}=\frac{\Delta x_{3}}{\Delta t_{3}}=\frac{4×(3.01^{2}-3^{2})}{3.01 - 3}m/s = 24.04m/s$。
(4)因为$\Delta t$越小所对应的平均速度越接近瞬时速度,所以$\overline{v}_{3}=24.04m/s$更接近$t_{1}=3s$时刻的瞬时速度大小。
(1)32 m/s
(2)24.4 m/s
(3)24.04 m/s
(4)见解析
(1)$\overline{v}_{1}=\frac{\Delta x_{1}}{\Delta t_{1}}=\frac{4×(5^{2}-3^{2})}{5 - 3}m/s = 32m/s$。
(2)$\overline{v}_{2}=\frac{\Delta x_{2}}{\Delta t_{2}}=\frac{4×(3.1^{2}-3^{2})}{3.1 - 3}m/s = 24.4m/s$。
(3)$\overline{v}_{3}=\frac{\Delta x_{3}}{\Delta t_{3}}=\frac{4×(3.01^{2}-3^{2})}{3.01 - 3}m/s = 24.04m/s$。
(4)因为$\Delta t$越小所对应的平均速度越接近瞬时速度,所以$\overline{v}_{3}=24.04m/s$更接近$t_{1}=3s$时刻的瞬时速度大小。
查看更多完整答案,请扫码查看


