《2025年天星教育28天预习新高一物理》

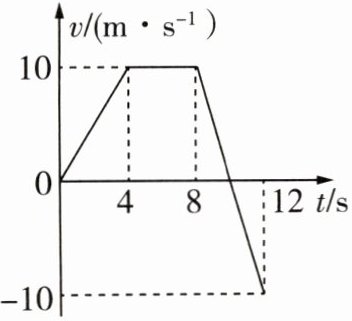
1.如图所示是某质点运动的$v - t$图像,请回答：
(1)质点在$4 \sim 8 s$、$10 \sim 12 s$内做什么性质的运动？
(2)在$0 \sim 4 s$、$8 \sim 10 s$、$10 \sim 12 s$内质点的加速度各是多少？
(3)质点在$0 \sim 12 s$内的路程和位移分别是多少？

答案： 1.
(1) 见解析　　
(2) $2.5m/s^{2},-5m/s^{2},-5m/s^{2}$
(3) $80m,60m$
(1) 质点在 $4\sim8s$ 内沿正方向做匀速直线运动，在 $10\sim12s$ 内沿负方向做匀加速直线运动。
(2) 根据 $v - t$ 图像的斜率表示加速度可得
$0\sim4s$ 内的加速度 $a_{1}=\frac{10 - 0}{4 - 0}m/s^{2}=2.5m/s^{2}$
$8\sim10s$ 内的加速度 $a_{2}=\frac{0 - 10}{10 - 8}m/s^{2}=-5m/s^{2}$
$10\sim12s$ 内的加速度 $a_{3}=\frac{-10 - 0}{12 - 10}m/s^{2}=-5m/s^{2}$。
(3) 根据 $v - t$ 图像与时间轴所围面积表示位移可知，质点在 $8\sim10s$ 和 $10\sim12s$ 内的位移大小相等，方向相反，则质点在 $0\sim12s$ 内的位移和 $0\sim8s$ 内的位移相同，即 $x=\frac{4 + 8}{2}×10m=60m$
在 $v - t$ 图像中，路程为所有位移的大小之和，所以路程为
【明思路】质点的总位移等于各部分位移的矢量和；质点通过的路程为图像与 $t$ 轴所围“面积”绝对值之和。
$s=\frac{4 + 10}{2}×10m+\frac{2×10}{2}m=80m$。

典例2 一辆汽车以初速度$v_0 = 25 m/s$,在平直的公路上匀速行驶,驾驶员突然发现较远的前方堵车,于是开始刹车,最后$1 s的位移为2.5 m$,求：
(1)刹车时加速度的大小；
(2)刹车开始后最初$2 s$内的平均速度大小；
(3)刹车后$6 s$内的位移大小。
解析 (1)汽车最后$1 s的位移为2.5 m$,由逆向思维可【破题点】末速度为0的匀减速直线运动,可逆向看成初速度为0的匀加速直线运动。
得$x_1 = \frac{1}{2}at_1^2$
解得汽车加速度大小为$a = \frac{2x_1}{t_1^2} = 5 m/s^2$。
(2)由匀变速直线运动的位移公式可得,汽车前$2 s内的位移为x_2 = v_0t_2 - \frac{1}{2}at_2^2 = 40 m$
所以前$2 s内的平均速度为v_1 = \frac{x_2}{t_2} = 20 m/s$。
(3)设汽车经过时间$t_0$速度减小为零【敲黑板】高频易错,很多初学者容易直接将$t = 6 s$代入公式而致错,刹车问题需要注意刹车时间。
则$t_0 = \frac{v_0}{a} = 5 s ＜ 6 s$
$5 s$末汽车已经停下,所以刹车后$6 s$内的位移大小为
$x_3 = v_0t_0 - \frac{1}{2}at_0^2 = 62.5 m$。

答案：
(1)解：将汽车刹车最后1s的运动逆向看作初速度为0的匀加速直线运动，由位移公式$x_{1}=\frac{1}{2}at_{1}^{2}$得，加速度大小$a=\frac{2x_{1}}{t_{1}^{2}}=\frac{2×2.5}{1^{2}}m/s^{2}=5m/s^{2}$。
(2)解：刹车开始后最初2s内的位移$x_{2}=v_{0}t_{2}-\frac{1}{2}at_{2}^{2}=25×2m-\frac{1}{2}×5×2^{2}m=40m$，平均速度$\overline{v}=\frac{x_{2}}{t_{2}}=\frac{40}{2}m/s=20m/s$。
(3)解：汽车刹车至停止的时间$t_{0}=\frac{v_{0}}{a}=\frac{25}{5}s=5s＜6s$，刹车后6s内的位移等于5s内的位移，$x_{3}=v_{0}t_{0}-\frac{1}{2}at_{0}^{2}=25×5m-\frac{1}{2}×5×5^{2}m=62.5m$。
答案：
(1)$5m/s^{2}$；
(2)$20m/s$；
(3)$62.5m$

2.一辆汽车在平直公路上以$4 m/s^2$的加速度加速行驶,加速后第$1秒内的位移为4 m$,求：
(1)汽车开始加速时的初速度大小$v_0$；
(2)汽车加速后$5 s内的位移大小x$。

答案： 2.
(1) $2m/s$
(2) $60m$
(1) 汽车做匀加速直线运动，由位移公式有
$x_{1}=v_{0}t_{1}+\frac{1}{2}at_{1}^{2}$
汽车的加速度大小 $a = 4m/s^{2}$，在 $t_{1}=1s$ 时间内行驶的距离 $x_{1}=4m$
代入数据解得汽车开始加速时的初速度大小 $v_{0}=2m/s$。
(2) 汽车加速运动的时间为 $t = 5s$
由匀变速直线运动公式可得，汽车加速后 $5s$ 内的位移大小为
$x=v_{0}t+\frac{1}{2}at^{2}=60m$。