《2025年1课3练单元达标测试六年级数学上册苏教版》

1. 计算下面物体的体积。

答案： 30×18×13=7020(cm³)
16×16×16=4096(cm³)
[提示]长方体的体积=长×宽×高，
正方体的体积=棱长×棱长×棱长。

2. 下面两个图形分别表示一个长方体的前面和右面,这个长方体的体积是(A)。

$A. 36 cm^3$
$B. 12 cm^3$
$C. 18 cm^3$

答案： A [提示]本题考查的是长方体体积的计算。先根据所给图形确定长方体的长、宽、高，再根据长方体体积计算公式计算。

3. 如右图,把一块石头浸没在一个棱长为6分米的正方体容器里,水面的高度由3.4分米上升到4分米。这块石头的体积是多少立方分米？

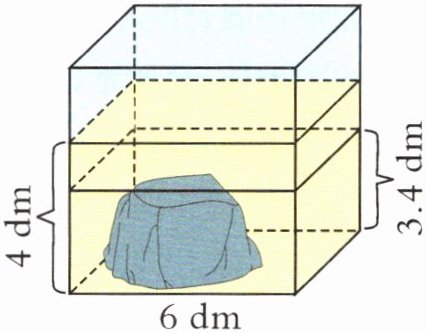
答案： 6×6×(4-3.4)=21.6(立方分米)
[提示]水上升部分的体积就是石头的体积，用容器的底面积乘水面上升的高度即可解答。

4. 方糖是用细晶粒精制砂糖为原料压制成的半方块状(即正方体的一半)的高级糖产品。它的特点是质量纯净,洁白而有光泽；糖块棱角完整,不易碎裂；在水中能够快速溶解,溶液清晰透明。已知一块方糖的底面是一个边长1.8厘米的正方形,则它的体积是多少立方厘米？

答案： 1.8×1.8×1.8÷2=2.916(立方厘米)
[提示]求方糖的体积就是求棱长1.8厘米的正方体体积的一半。

5. 原创题 空间观念 学习“蜡烛的变化”时,小华所在的小组做了一支蜡烛。将一块棱长6厘米的正方体蜡块熔化,放入一个长3厘米、宽2.5厘米的长方体模具,制作成蜡烛。
(1)实验发现：在制作蜡烛的过程中,蜡块仅仅是(形状)发生了变化。
(2)制作成的蜡烛的高是多少厘米？(损耗忽略不计)
6×6×6÷(3×2.5)=28.8(厘米)

答案：
(1)形状
(2)6×6×6÷(3×2.5)=28.8(厘米)