《2025年1课3练单元达标测试六年级数学上册苏教版》

1. 某种书先提价$\frac{1}{6}$,又降价$\frac{1}{6}$,这种书的原价(高于)现价,(填“高于”“低于”或“等于”),如果先提价$\frac{1}{6}$,再降价$\frac{(1)}{(7)}$,那么现价和原价就一样了。

答案： 高于 $\frac{1}{7}$
[提示]第 1 问可采用假设法。假设这种书的原价是 1 元，算出现价后再和原价相比，确定是原价高还是现价高。第 2 问假设原价和现价均是 1 元，先提价 $\frac{1}{6}$，则提价后的价格是 $1×(1+\frac{1}{6})=\frac{7}{6}$（元），再降价，降价后的价格是 1 元，则降了 $(\frac{7}{6}-1)÷\frac{7}{6}=\frac{1}{7}$。

2. 看图列式计算。
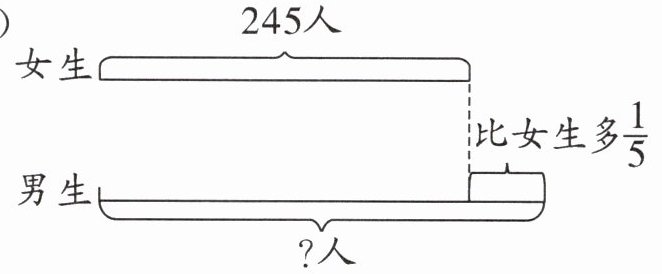
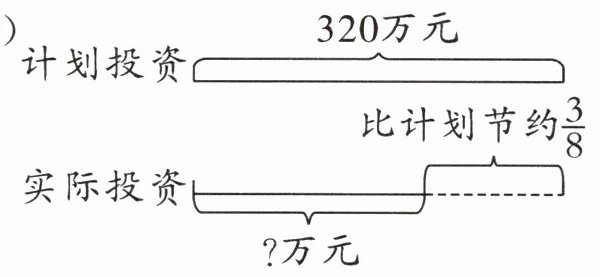
(1)
(2)

答案：
(1)$245×(1+\frac{1}{5})=294$（人）
[提示]根据题意可知，女生有 245 人，男生的人数比女生多 $\frac{1}{5}$，是把女生人数看作单位“1”，男生人数相当于女生人数的 $(1+\frac{1}{5})$，用女生人数乘 $(1+\frac{1}{5})$就是男生人数。
(2)$320×(1-\frac{3}{8})=200$（万元） [提示]根据题意可知，计划投资 320 万元，实际投资的钱数比计划节约 $\frac{3}{8}$，是把计划投资的钱数看作单位“1”，实际投资的钱数相当于计划投资的 $(1-\frac{3}{8})$，用计划投资的钱数乘 $(1-\frac{3}{8})$，就是实际投资的钱数。

3. 狮子每小时能跑60千米,猎豹每小时能跑多少千米?

答案： $60×(1+\frac{3}{5})=96$（千米） [提示]根据题意可知，狮子每小时跑 60 千米，猎豹的奔跑速度比狮子快 $\frac{3}{5}$，是把狮子的奔跑速度看作单位“1”，猎豹的奔跑速度相当于狮子的 $(1+\frac{3}{5})$，用狮子每小时奔跑的路程乘 $(1+\frac{3}{5})$，就是猎豹每小时奔跑的路程。

4. 在动物的生命历程中,牙齿起着至关重要的作用。不同动物的牙齿数不同。其中猫有30颗牙齿,母马的牙齿数是猫的$\frac{6}{5}$,狗的牙齿数比母马多$\frac{1}{6}$。狗有多少颗牙齿?

答案： 母马：$30×\frac{6}{5}=36$（颗） 狗：$36×(1+\frac{1}{6})=42$（颗）

5. 原创题 量感 《三国演义》是中国文学史上第一部章回体小说,是历史演义小说的开山之作。小明买了一本360页的《三国演义》,第一周读了整本书的$\frac{1}{4}$,第二周读的页数比第一周读后剩下的页数少$\frac{5}{9}$。小明第三周应从第几页读起?
第三周开始读起的页数= 第一周读的页数+第二周读的页数+1

答案： $360×\frac{1}{4}=90$（页）
$(360 - 90)×(1-\frac{5}{9})=120$（页）
$90 + 120 + 1=211$（页）
[提示]先根据“第一周读了整本书的 $\frac{1}{4}$”，单位“1”是全书的页数，用全书的页数 $×\frac{1}{4} =$第一周读的页数；再根据“第二周读的页数比第一周读后剩下的页数少 $\frac{5}{9}$”，单位“1”是第一周读后剩下的页数，求出第一周读后剩下的页数，用第一周读后剩下的页数 $×(1-\frac{5}{9})=$第二周读的页数；最后用第一、二周读的页数之和加 1 求出第三周开始读的页数。
易错提醒 不同的单位“1”
题目中的单位“1”是不一样的，第一次书的总页数是单位“1”，第二次第一周读后剩下的页数是单位“1”。单位“1”变化的应用题一定要弄清楚每一个分率对应的单位“1”。