《2025年1课3练单元达标测试六年级数学上册苏教版》

1. 计算下面物体的体积。

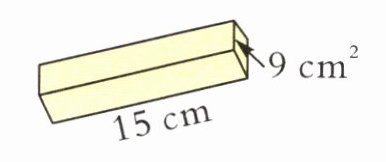
答案： 9×15=135(cm³)
0.2×5=1(m³)
[提示]根据长方体体积=底面积×高,把相应数据代入公式计算即可。

2. 把一根长 12 米的长方体木材锯成完全相同的两根小长方体木材(如右下图),表面积增加了0.8 平方分米。这根木材原来的体积是多少立方米?

答案： 0.8平方分米=0.008平方米
0.008÷2×12=0.048(立方米)

3. 如果将展开的军被和叠好的军被看作长方体,展开的军被长 200 厘米,宽 150 厘米,厚 25 毫米;叠好后的军被长 60 厘米,宽 50 厘米,那么叠好后的军被厚度大约是多少? (军被体积变化忽略不计)

答案： 25毫米=2.5厘米
200×150×2.5÷(60×50)=25(厘米)
[提示]军被折叠前后体积不变。注意单位的换算。

4. 如右下图,一个长方体的长是 12 厘米,高是 8 厘米,涂色部分的两个面的面积之和是 200 平方厘米。这个长方体的体积是多少立方厘米?

答案： 200÷(12+8)=10(厘米)
12×8×10=960(立方厘米)

5. 新考法 图形探究 点移动成线,线移动成面,面移动成体。因此长方体可看作是面的平移叠加。

(1)一张长方形硬纸板的面积是 12 平方厘米,竖直摆放后向右平移 5 厘米,形成的长方体的体积是(60)立方厘米。
(2)一张周长是 20 厘米的正方形硬纸板向右平移一定的距离后,若形成的长方体的体积是 60 立方厘米,则它向右平移了(2.4)厘米。
把硬纸板看作是长方体的底面,则向右移动的距离相当于长方体的高。

答案：
(1)60 [提示]形成的长方体的底面积是12平方厘米,长是5厘米,求它的体积直接用底面积×长,即12×5=60(立方厘米)。
(2)2.4 [提示]长方体的体积÷底面积=长,即向右平移的厘米数。先根据正方形的周长求出边长,再求出面积,即长方体的底面积,最后求出它的长。