《2025年1课3练单元达标测试六年级数学上册苏教版》

1 用相差关系和倍比关系解决问题。
例 李阿姨的服装店昨天卖出一种上衣 3 件,一种裤子 5 件。每件上衣比每条裤子贵 50 元,一共收入 950 元,上衣和裤子的单价各多少元？
思路分析 每件上衣比每条裤子贵 50 元,可以将上衣替换为裤子,则 3 件上衣就少了 3×50＝150(元),这时总价也少了 150 元,变成 950－150＝800(元),相当于 800 元买了 8 条裤子；也可以将裤子替换成上衣,这时总价多了 5×50＝250(元),相当于买 8 件上衣需要 950＋250＝1200(元)。
解答 方法一：裤子：(950－50×3)÷(5＋3)＝100(元) 上衣：100＋50＝150(元)
方法二：上衣：(950＋50×5)÷(5＋3)＝150(元) 裤子：150－50＝100(元)
答：一件上衣 150 元,一条裤子 100 元。

答案： 上衣 150 元,裤子 100 元。

1. 如右下图,玩具熊的单价是玩具飞机的$\frac{1}{3}$。玩具熊和玩具飞机的单价各是多少元。

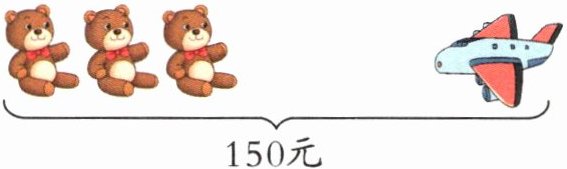
答案： 玩具飞机：150÷(3÷3+1)=75(元)
玩具熊：75×$\frac{1}{3}$=25(元)

2 根据数量关系将多个未知量转化为一个未知量。
例 有三块铁块,共重 4 千克,已知第二块比第一块轻 400 克,第三块的质量是第二块的 2 倍。求每块铁块各重多少克。
思路分析 本题中有三个未知量,但这三个未知量中有一个公共量,第一块、第三块铁块的质量都和第二块铁块的质量有关系,可以将第一块、第三块铁块的质量都转化为第二块铁块的质量,已知第二块比第一块轻 400 克,则第一块比第二块重 400 克,将第一块的质量去掉 400 克就与第二块同样重了,这时三块铁块的总质量也相应减少 400 克。第三块的质量是第二块的 2 倍,把第三块的质量看作 2 份的第二块的质量,此时相当于总质量是 4000－400＝3600(克),总份数为 1＋1＋2＝4(份),可以求出 1 份的质量,即第二块的质量,再求出其余两块的质量。
解答 4 千克＝4000 克 第二块：(4000－400)÷(1＋1＋2)＝900(克)
第一块：900＋400＝1300(克) 第三块：900×2＝1800(克)
答：第一块铁块重 1300 克,第二块铁块重 900 克,第三块铁块重 1800 克。

答案： 4千克＝4000克
第二块：(4000－400)÷(1＋1＋2)＝900(克)
第一块：900＋400＝1300(克)
第三块：900×2＝1800(克)
答：第一块铁块重1300克，第二块铁块重900克，第三块铁块重1800克。