《2025年初中生暑假生活七年级综合全一册人教版》

1. 将三角形各顶点的纵坐标分别减 5, 横坐标不变, 连接这三个新点所成的三角形与原图形相比( ).

A.向右平移了 5 个单位长度
B.向左平移了 5 个单位长度
C.向上平移了 5 个单位长度
D.向下平移了 5 个单位长度

答案： 在平面直角坐标系中，图形的平移规律为：横坐标变化影响左右平移（左减右加），纵坐标变化影响上下平移（上加下减）。
原三角形各顶点纵坐标减5，横坐标不变，根据平移规律，相当于将原三角形向下平移了5个单位长度。
D

2. 已知点 $ P(3+m,2n) $ 与点 $ Q(2m-3,2n+1) $, 直线 $ PQ // y $ 轴, 则 $ m,n $ 的值分别为( ).

A.$ m= -6,n $ 为任意数
B.$ m= -2,n= 0 $
C.$ m= 6,n $ 为任意数
D.$ m= 2,n= 0 $

答案： 解：
∵直线PQ//y轴，
∴点P与点Q的横坐标相等，纵坐标不相等。
∴3+m=2m-3，
解得m=6。
又
∵2n≠2n+1，该式恒成立，
∴n为任意数。
综上，m=6，n为任意数。
答案：C

3. 在平面直角坐标系中, 将坐标为 $ (5,6),(1,2),(3,2),(3,0),(7,0),(7,2),(9,2),(5,6) $ 的点用线段依次连接起来形成一个图案, 然后按照下面的要求作出新的图案.
(1) 纵坐标保持不变, 横坐标分别减 3;
(2) 横坐标分别加 2, 纵坐标分别减 3.

答案：
(1)解：新图案各点坐标依次为(2,6),(-2,2),(0,2),(0,0),(4,0),(4,2),(6,2),(2,6)。
(2)解：新图案各点坐标依次为(7,3),(3,-1),(5,-1),(5,-3),(9,-3),(9,-1),(11,-1),(7,3)。

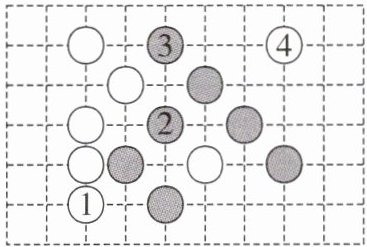
4. 五子棋的比赛规则是同色五子谁先形成一条直线谁获胜. 如图所示的是两人玩的一盘五子棋, 若棋盘上白棋①的坐标为 $ (-3,-2) $, 黑棋②的坐标为 $ (-1,0) $.
(1) 请你根据题意, 画出相应的平面直角坐标系;
(2) 分别写出黑棋③和白棋④的坐标;
(3) 现轮到黑棋下, 要使黑棋这一步就获胜,黑棋应该下在哪? 请写出这一步黑棋的坐标.

答案：

(1)
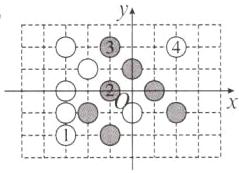
(2)黑棋③的坐标为(-1,2),白棋④的坐标为(2,2).
(3)(3,-2)或(-2,3).