《2025年天舟文化精彩暑假团结出版社八年级数学湘教版》

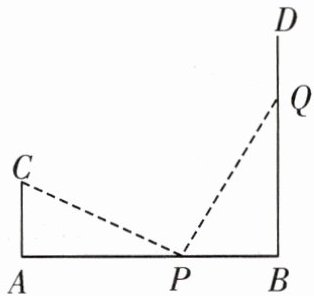
6. 如图,$AB= 12m,CA⊥AB$于A,$DB⊥AB$于B,且$AC= 4m$,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P,Q两点同时出发,运动4min后,$△CAP与△PQB$全等.

答案： 解：设运动 $ t $ min 后，$\triangle CAP$ 与 $\triangle PQB$ 全等。
由题意得：$BP = t$ m，$BQ = 2t$ m，$AP = AB - BP = (12 - t)$ m。
因为 $CA \perp AB$，$DB \perp AB$，所以 $\angle A = \angle B = 90^\circ$。
若 $\triangle CAP \cong \triangle PBQ$，则需满足：
$\begin{cases} AC = BP \\ AP = BQ \end{cases}$
即 $\begin{cases} 4 = t \\ 12 - t = 2t \end{cases}$
解得 $t = 4$，且 $12 - 4 = 8 = 2×4$，符合题意。
若 $\triangle CAP \cong \triangle QBP$，则需满足：
$\begin{cases} AC = BQ \\ AP = BP \end{cases}$
即 $\begin{cases} 4 = 2t \\ 12 - t = t \end{cases}$
解得 $t = 2$ 且 $t = 6$，矛盾，舍去。
综上，$t = 4$。
4

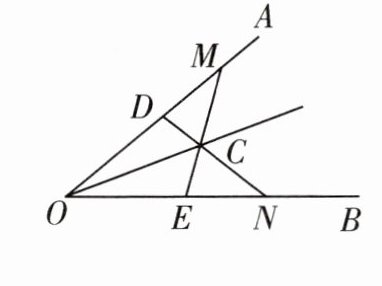
7. 如图,在$∠AOB$的两边OA,OB上分别取$OM= ON,OD= OE$,DN和EM相交于点C.求证:OC平分$∠AOB$.

答案： 证明：在△OME和△OND中，
∵OM=ON，∠MOE=∠NOD，OE=OD，
∴△OME≌△OND（SAS），
∴∠OME=∠OND。
∵OM=ON，OD=OE，
∴MD=NE。
在△MCD和△NCE中，
∵∠MCD=∠NCE，∠CMD=∠CNE，MD=NE，
∴△MCD≌△NCE（AAS），
∴CD=CE。
在△OCD和△OCE中，
∵OD=OE，CD=CE，OC=OC，
∴△OCD≌△OCE（SSS），
∴∠COD=∠COE，
即OC平分∠AOB。

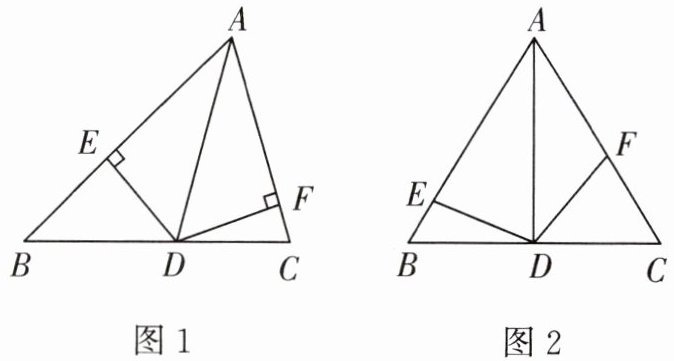
在$△ABC$中,若AD是$∠BAC$的平分线,点E和点F分别在AB和AC上,且$DE⊥AB$,垂足为E,$DF⊥AC$,垂足为F(如图1),则可以得到以下两个结论:
①$∠AED+∠AFD= 180^{\circ }$;②$DE= DF$.
那么在$△ABC$中,仍然有条件“AD是$∠BAC$的平分线,点E和点F分别在AB和AC上”,请探究以下两个问题:
(1)若$∠AED+∠AFD= 180^{\circ }$(如图2),则DE与DF是否仍相等?若相等,请证明;否则请举出反例.
(2)若$DE= DF$,则$∠AED+∠AFD= 180^{\circ }$是否成立?(只写出结论,不证明)

答案：
(1)解：DE=DF。
证明：过点D作DM⊥AB于M，DN⊥AC于N。
∵AD平分∠BAC，DM⊥AB，DN⊥AC，
∴DM=DN，∠DME=∠DNF=90°。
∵∠AED+∠AFD=180°，∠AED+∠DEM=180°，
∴∠DEM=∠AFD。
在△DEM和△DFN中，
∠DEM=∠DFN，∠DME=∠DNF，DM=DN，
∴△DEM≌△DFN(AAS)，
∴DE=DF。
(2)不成立。