《2025年天舟文化精彩暑假团结出版社八年级数学湘教版》

7.已知点$P(2a-10,1-a)$位于第三象限,点$Q(x,y)$位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为-3,试求出a的值.
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标.
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.

答案：
(1)解：因为点P的纵坐标为-3，所以1-a=-3，解得a=4。
(2)解：由
(1)知a=4，则点P的横坐标为2×4-10=-2，所以P(-2,-3)。点Q位于第二象限且由P向上平移得到，设向上平移k(k＞0)个单位，则Q(-2,-3+k)。因为Q在第二象限，所以-3+k＞0，即k＞3，取k=4，得Q(-2,1)（答案不唯一）。
(3)解：因为点P(2a-10,1-a)在第三象限，所以$\begin{cases}2a-10＜0 \\1-a＜0\end{cases}$，解得1＜a＜5。因为横、纵坐标都是整数，所以a=2,3,4。当a=2时，P(-6,-1)；a=3时，P(-4,-2)；a=4时，P(-2,-3)。点Q在第二象限且由P向上平移得到，设平移距离为m(m＞0)，则Q的横坐标与P相同，纵坐标为(1-a)+m＞0，即m＞a-1。线段PQ长度为m，所以PQ＞ a-1。当a=2时，PQ＞1；a=3时，PQ＞2；a=4时，PQ＞3。综上，a=2,3,4；当a=2时，PQ＞1；a=3时，PQ＞2；a=4时，PQ＞3。

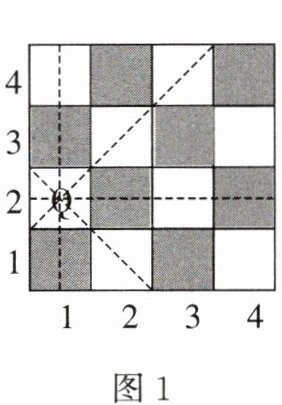
国际象棋、中国象棋和围棋号称世界三大棋种.国际象棋中“后”的威力可比中国象棋中“车”大得多:“后”不仅能控制其所在的行与列中的每一个小方格,还能控制“斜”方向的两条直线上的每一个小方格.图1是一个$4×4$的小方格棋盘,图中的“后Q”能控制图中虚线所经过的每一个小方格.



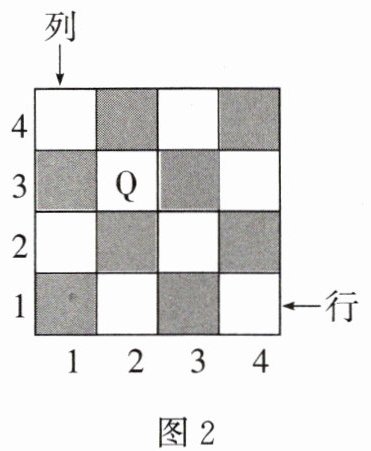
(1)在图2所示的小方格棋盘中有一“后Q”,其所在的位置可用“$(2,3)$”来表示,请说明“后Q”所在的位置“$(2,3)$”的意义,并用这种表示方法分别写出棋盘中不能被该“后Q”所控制的四个位置.
(2)图3也是一个$4×4$的小方格棋盘,请在这个棋盘中放入四个“后Q”,使这四个“后Q”之间互不受对方控制(在图3中的某四个小方格中标出字母Q即可).

答案： 【解析】：
(1)位置“(2,3)”表示“后Q”位于第2列第3行。
根据“后Q”的控制规则，它能控制所在行、列以及斜方向直线上的所有方格。
在4×4的棋盘中，
“后Q”位于(2,3)，
它能控制第2列的所有方格（即(2,1)，(2,2)，(2,4)），
第3行的所有方格（即(1,3)，(3,3)，(4,3)），
以及斜方向上的方格（即(1,2)，(1,4)，(3,2)，(3,4)，(4,1)，(4,4)中的部分，但由于棋盘边界，实际控制的是(1,2)，(1,4)，(3,2)，(4,4)）。
因此，不能被该“后Q”所控制的四个位置是(3,1)，(4,1)，(3,4)，(4,2)（答案不唯一，只要写出四个不被控制的位置即可）。
(2)要在4×4的棋盘中放入四个“后Q”，使它们之间互不受对方控制，
需要确保每个“后Q”都不在同一行、同一列或同一斜方向上。
一种可能的放置方式是：
在(1,1)，(2,3)，(3,4)，(4,2)位置放置“后Q”。
这样，每个“后Q”都控制不同的行、列和斜方向，从而满足条件。
【答案】：
(1)“后Q”所在的位置“(2,3)”的意义是“后Q”位于第2列第3行；
不能被该“后Q”所控制的四个位置是(3,1)，(4,1)，(3,4)，(4,2)（答案不唯一）。
(2)在图3的棋盘中，可以在(1,1)，(2,3)，(3,4)，(4,2)位置放置“后Q”，使这四个“后Q”之间互不受对方控制。（图略，在对应位置标出Q即可）。