《2025年天舟文化精彩暑假团结出版社八年级数学湘教版》

1. 已知点$A(2,-5)$,若$AB平行于y$轴,则点$B$的坐标可能是 (B)
A.$(-2,5)$
B.$(2,6)$
C.$(5,-5)$
D.$(-5,5)$

答案： 【解析】：
本题主要考查了平行于坐标轴的直线上点的坐标特点。
在平面直角坐标系中，平行于$y$轴的直线上的所有点的横坐标都相同。
已知点$A(2,-5)$，且线段$AB$平行于$y$轴，那么点$B$的横坐标必须与点$A$的横坐标相同，即点$B$的横坐标必须为$2$。
接下来，逐一检查选项：
A. $(-2,5)$ 的横坐标不为$2$，故A选项错误；
B. $(2,6)$ 的横坐标为$2$，与点$A$的横坐标相同，故B选项正确；
C. $(5,-5)$ 的横坐标不为$2$，故C选项错误；
D. $(-5,5)$ 的横坐标不为$2$，故D选项错误。
【答案】：B

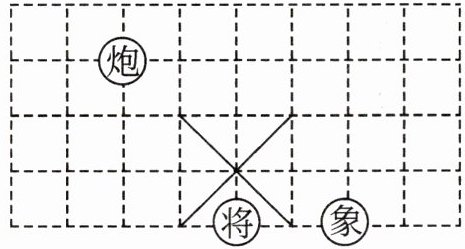
2. 如图,若在象棋盘上建立直角坐标系,使“将”位于点$(1,-2)$,“象”位于点$(3,-2)$,则“炮”位于 (B)

A.点$(1,-1)$
B.点$(-1,1)$
C.点$(-1,2)$
D.点$(1,-2)$

答案： 解：由“将”位于点$(1,-2)$，“象”位于点$(3,-2)$，可知两点在同一水平线上，相距2个单位长度，对应象棋盘上2格，故每个小方格边长为1个单位长度，向右为x轴正方向，向上为y轴正方向。
“将”在第1列第-2行，向左数2格为“炮”所在列，即$1 - 2 = -1$；向上数3格为“炮”所在行，即$-2 + 3 = 1$。
所以“炮”位于点$(-1,1)$。
答案：B

3. 要把点$(-2,5)$平移到x轴上,则下列方法中可行的是 (A)
A.横坐标不变,纵坐标减去5
B.横坐标不变,纵坐标减去2
C.纵坐标不变,横坐标加上5
D.纵坐标不变,横坐标加上2

答案： 【解析】：
该问题考查的是点的平移性质。在平面直角坐标系中，一个点在x轴上的特点是其纵坐标为0。因此，要把点$(-2,5)$平移到x轴上，我们需要改变其纵坐标，使其变为0，而横坐标可以不变。
A选项：横坐标不变，纵坐标减去5。原点的纵坐标为5，减去5后变为0，满足条件。
B选项：横坐标不变，纵坐标减去2。减去2后纵坐标变为3，不满足条件。
C选项：纵坐标不变，横坐标加上5。这只会改变点的横坐标，纵坐标不变，不满足条件。
D选项：纵坐标不变，横坐标加上2。同样只改变横坐标，不满足条件。
【答案】：
A