1. 一个多边形内角和是$1080^{\circ }$,则这个多边形的对角线条数为 (
A.20
B.22
C.25
D.27
A
)A.20
B.22
C.25
D.27
答案:
【解析】:
首先,根据多边形的内角和公式 $(n-2) × 180^{\circ}$,我们可以求出多边形的边数 $n$。
已知内角和为 $1080^{\circ}$,则有:
$(n-2) × 180^{\circ} = 1080^{\circ}$,
解这个方程,我们得到:
$n-2 = 6$,
$n = 8$,
所以,这个多边形是一个八边形。
接下来,我们需要求出八边形的对角线条数。
对于一个 $n$ 边形,其对角线的条数可以用公式 $\frac{n(n-3)}{2}$ 来计算。
将 $n = 8$ 代入公式,我们得到:
$\frac{8 × (8-3)}{2} = \frac{8 × 5}{2} = 20$,
所以,这个八边形的对角线条数是 20。
【答案】:A.20。
首先,根据多边形的内角和公式 $(n-2) × 180^{\circ}$,我们可以求出多边形的边数 $n$。
已知内角和为 $1080^{\circ}$,则有:
$(n-2) × 180^{\circ} = 1080^{\circ}$,
解这个方程,我们得到:
$n-2 = 6$,
$n = 8$,
所以,这个多边形是一个八边形。
接下来,我们需要求出八边形的对角线条数。
对于一个 $n$ 边形,其对角线的条数可以用公式 $\frac{n(n-3)}{2}$ 来计算。
将 $n = 8$ 代入公式,我们得到:
$\frac{8 × (8-3)}{2} = \frac{8 × 5}{2} = 20$,
所以,这个八边形的对角线条数是 20。
【答案】:A.20。
2. 如图,$□ABCD$的周长为 20 cm,$AB≠AD$,AC,BD 相交于点 O,$OE⊥BD$交 AD 于点 E,则$△ABE$的周长为 (
A.4 cm
B.6 cm
C.8 cm
D.10 cm
D
)A.4 cm
B.6 cm
C.8 cm
D.10 cm
答案:
解:
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OB=OD。
∵平行四边形ABCD的周长为20cm,
∴AB+AD=10cm。
∵OE⊥BD,OB=OD,
∴OE垂直平分BD,
∴BE=DE。
∴△ABE的周长=AB+AE+BE=AB+AE+DE=AB+AD=10cm。
答案:D
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OB=OD。
∵平行四边形ABCD的周长为20cm,
∴AB+AD=10cm。
∵OE⊥BD,OB=OD,
∴OE垂直平分BD,
∴BE=DE。
∴△ABE的周长=AB+AE+BE=AB+AE+DE=AB+AD=10cm。
答案:D
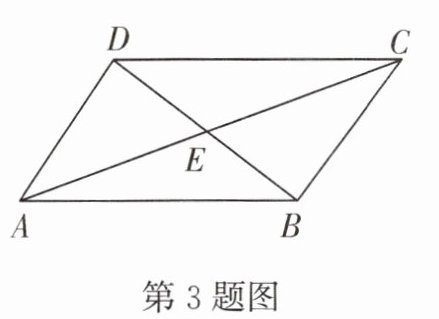
3. 如图,在四边形 ABCD 中,对角线 AC,BD 相交于点 E,$∠CBD= 90^{\circ }$,$BC= 4,BE= ED= 3,AC= 10$,则四边形 ABCD 的面积为 (
A.6
B.12
C.20
D.24
D
)
A.6
B.12
C.20
D.24
答案:
解:在Rt△BEC中,∠CBD=90°,BC=4,BE=3,
由勾股定理得:CE=$\sqrt{BC^{2}+BE^{2}}=\sqrt{4^{2}+3^{2}}=5$。
∵AC=10,
∴AE=AC-CE=10-5=5。
∴AE=CE=5,又BE=ED=3,
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形)。
∵BD=BE+ED=6,
∴S四边形ABCD=2S△BCD。
在Rt△BCD中,∠CBD=90°,BC=4,BD=6,
S△BCD=$\frac{1}{2}×BD×BC=\frac{1}{2}×6×4=12$,
∴S四边形ABCD=2×12=24。
答案:D
由勾股定理得:CE=$\sqrt{BC^{2}+BE^{2}}=\sqrt{4^{2}+3^{2}}=5$。
∵AC=10,
∴AE=AC-CE=10-5=5。
∴AE=CE=5,又BE=ED=3,
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形)。
∵BD=BE+ED=6,
∴S四边形ABCD=2S△BCD。
在Rt△BCD中,∠CBD=90°,BC=4,BD=6,
S△BCD=$\frac{1}{2}×BD×BC=\frac{1}{2}×6×4=12$,
∴S四边形ABCD=2×12=24。
答案:D
4. 如图,D 是$△ABC$内一点,$BD⊥CD,AD= 6,BD= 4,$$CD= 3$,E,F,G,H 分别是 AB,AC,CD,BD 的中点,则四边形 EFGH 的周长是 (
A.7
B.9
C.10
D.11
D
)A.7
B.9
C.10
D.11
答案:
【解析】:本题可先根据勾股定理求出$BC$的长度,再利用三角形中位线定理求出四边形$EFGH$各边的长度,进而求出其周长。
步骤一:求$BC$的长度
已知$BD\perp CD$,$BD = 4$,$CD = 3$,在$Rt\triangle BCD$中,根据勾股定理$a^2+b^2=c^2$(其中$a$、$b$为直角边,$c$为斜边),可得:
$BC=\sqrt{BD^{2}+CD^{2}}=\sqrt{4^{2}+3^{2}}=\sqrt{16 + 9}=\sqrt{25}=5$
步骤二:利用三角形中位线定理求四边形$EFGH$各边的长度
因为$E$、$H$分别是$AB$、$BD$的中点,根据三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半。所以$EH$是$\triangle ABD$的中位线,则$EH=\frac{1}{2}AD$。
已知$AD = 6$,所以$EH=\frac{1}{2}×6 = 3$。
同理,$F$、$G$分别是$AC$、$CD$的中点,$FG$是$\triangle ACD$的中位线,则$FG=\frac{1}{2}AD = 3$。
$E$、$F$分别是$AB$、$AC$的中点,$EF$是$\triangle ABC$的中位线,则$EF=\frac{1}{2}BC$。
由步骤一可知$BC = 5$,所以$EF=\frac{1}{2}×5 = 2.5$。
$H$、$G$分别是$BD$、$CD$的中点,$HG$是$\triangle BCD$的中位线,则$HG=\frac{1}{2}BC = 2.5$。
步骤三:求四边形$EFGH$的周长
四边形$EFGH$的周长为$EH + FG + EF + HG$,将$EH = 3$,$FG = 3$,$EF = 2.5$,$HG = 2.5$代入可得:
$3 + 3 + 2.5 + 2.5 = 11$
【答案】:D
步骤一:求$BC$的长度
已知$BD\perp CD$,$BD = 4$,$CD = 3$,在$Rt\triangle BCD$中,根据勾股定理$a^2+b^2=c^2$(其中$a$、$b$为直角边,$c$为斜边),可得:
$BC=\sqrt{BD^{2}+CD^{2}}=\sqrt{4^{2}+3^{2}}=\sqrt{16 + 9}=\sqrt{25}=5$
步骤二:利用三角形中位线定理求四边形$EFGH$各边的长度
因为$E$、$H$分别是$AB$、$BD$的中点,根据三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半。所以$EH$是$\triangle ABD$的中位线,则$EH=\frac{1}{2}AD$。
已知$AD = 6$,所以$EH=\frac{1}{2}×6 = 3$。
同理,$F$、$G$分别是$AC$、$CD$的中点,$FG$是$\triangle ACD$的中位线,则$FG=\frac{1}{2}AD = 3$。
$E$、$F$分别是$AB$、$AC$的中点,$EF$是$\triangle ABC$的中位线,则$EF=\frac{1}{2}BC$。
由步骤一可知$BC = 5$,所以$EF=\frac{1}{2}×5 = 2.5$。
$H$、$G$分别是$BD$、$CD$的中点,$HG$是$\triangle BCD$的中位线,则$HG=\frac{1}{2}BC = 2.5$。
步骤三:求四边形$EFGH$的周长
四边形$EFGH$的周长为$EH + FG + EF + HG$,将$EH = 3$,$FG = 3$,$EF = 2.5$,$HG = 2.5$代入可得:
$3 + 3 + 2.5 + 2.5 = 11$
【答案】:D
查看更多完整答案,请扫码查看


