1. 如果直角三角形的一个锐角是另一个锐角的4倍,那么这个锐角的度数是 (
A.$18^{\circ}$
B.$36^{\circ}$
C.$54^{\circ}$
D.$72^{\circ}$
D
)A.$18^{\circ}$
B.$36^{\circ}$
C.$54^{\circ}$
D.$72^{\circ}$
答案:
【解析】:
设直角三角形中较小的锐角为 $x$ 度,则另一个锐角为 $4x$ 度。
由于直角三角形的两个锐角之和为 $90^{\circ}$,所以有方程:
$x + 4x = 90^{\circ}$,
解这个方程,得到:
$5x = 90^{\circ}$,
$x = 18^{\circ}$,
但题目要求的是较大的锐角,即 $4x$,所以:
$4x = 72^{\circ}$。
【答案】:
D. $72^{\circ}$。
设直角三角形中较小的锐角为 $x$ 度,则另一个锐角为 $4x$ 度。
由于直角三角形的两个锐角之和为 $90^{\circ}$,所以有方程:
$x + 4x = 90^{\circ}$,
解这个方程,得到:
$5x = 90^{\circ}$,
$x = 18^{\circ}$,
但题目要求的是较大的锐角,即 $4x$,所以:
$4x = 72^{\circ}$。
【答案】:
D. $72^{\circ}$。
2. 如图,在$Rt△ABC$中,$∠C= 90^{\circ },∠A= 30^{\circ }$,D 为 AB 的中点,$DE⊥AC$于点 E,$AB= 8$,则 DE 的长度为 (
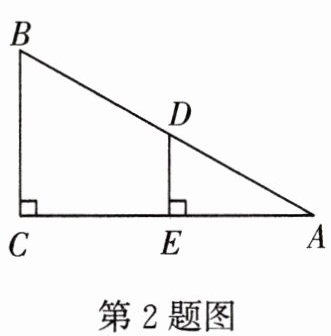
A.1
B.2
C.4
D.8
B
)
A.1
B.2
C.4
D.8
答案:
【解析】:
本题可先根据直角三角形斜边中线的性质求出$AD$的长度,再结合含$30^{\circ}$角的直角三角形的性质求出$DE$的长度。
步骤一:根据直角三角形斜边中线的性质求出$AD$的长度
在直角三角形中,斜边上的中线等于斜边的一半。
已知在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$D$为$AB$的中点,$AB = 8$,所以$AD=\frac{1}{2}AB=\frac{1}{2}×8 = 4$。
步骤二:根据含$30^{\circ}$角的直角三角形的性质求出$DE$的长度
因为$DE\perp AC$,所以$\angle AED = 90^{\circ}$。
在$Rt\triangle ADE$中,$\angle A = 30^{\circ}$,根据在直角三角形中,如果一个锐角等于$30^{\circ}$,那么它所对的直角边等于斜边的一半,可得$DE=\frac{1}{2}AD$。
由步骤一可知$AD = 4$,所以$DE=\frac{1}{2}×4 = 2$。
【答案】:B
本题可先根据直角三角形斜边中线的性质求出$AD$的长度,再结合含$30^{\circ}$角的直角三角形的性质求出$DE$的长度。
步骤一:根据直角三角形斜边中线的性质求出$AD$的长度
在直角三角形中,斜边上的中线等于斜边的一半。
已知在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$D$为$AB$的中点,$AB = 8$,所以$AD=\frac{1}{2}AB=\frac{1}{2}×8 = 4$。
步骤二:根据含$30^{\circ}$角的直角三角形的性质求出$DE$的长度
因为$DE\perp AC$,所以$\angle AED = 90^{\circ}$。
在$Rt\triangle ADE$中,$\angle A = 30^{\circ}$,根据在直角三角形中,如果一个锐角等于$30^{\circ}$,那么它所对的直角边等于斜边的一半,可得$DE=\frac{1}{2}AD$。
由步骤一可知$AD = 4$,所以$DE=\frac{1}{2}×4 = 2$。
【答案】:B
3. 如图,AD 是$△ABC$的中线,$∠ADC= 45^{\circ }$,把$△ADC$沿着直线 AD 对折,点 C 落在点 E 的位置,如果$BC= 6$,那么线段 BE 的长度为 ( )

A.6
B.$6\sqrt {2}$
C.$2\sqrt {3}$
D.$3\sqrt {2}$

A.6
B.$6\sqrt {2}$
C.$2\sqrt {3}$
D.$3\sqrt {2}$
答案:
【解析】:本题可先根据中线的性质求出$BD$的长度,再根据折叠的性质得到$DE$的长度以及$\angle EDA$的度数,进而求出$\angle EDB = 90^{\circ}$,最后在$Rt\triangle BDE$中利用勾股定理求出$BE$的长度。
步骤一:根据中线的性质求出$BD$的长度
已知$AD$是$\triangle ABC$的中线,根据三角形中线的定义:三角形的中线是连接三角形顶点和它的对边中点的线段,可得$D$为$BC$中点。
因为$BC = 6$,所以$BD=\dfrac{1}{2}BC=\dfrac{1}{2}×6 = 3$。
步骤二:根据折叠的性质求出$DE$的长度以及$\angle EDA$的度数
由于$\triangle ADC$沿着直线$AD$对折,点$C$落在点$E$的位置,根据折叠的性质:折叠前后的图形全等,可得$\triangle ADE\cong\triangle ADC$。
所以$DE = DC$,$\angle EDA=\angle ADC = 45^{\circ}$。
又因为$D$为$BC$中点,$BC = 6$,所以$DC=\dfrac{1}{2}BC = 3$,则$DE = 3$。
步骤三:求出$\angle EDB$的度数
因为$\angle EDA = 45^{\circ}$,$\angle ADC = 45^{\circ}$,且$\angle EDA+\angle ADC+\angle EDB = 180^{\circ}$,所以$\angle EDB = 180^{\circ}-\angle EDA - \angle ADC = 180^{\circ}- 45^{\circ}- 45^{\circ}= 90^{\circ}$。
步骤四:在$Rt\triangle BDE$中利用勾股定理求出$BE$的长度
在$Rt\triangle BDE$中,$\angle EDB = 90^{\circ}$,$BD = 3$,$DE = 3$,根据勾股定理:在任何一个直角三角形中,两条直角边长的平方和等于斜边长的平方,即$a^2 + b^2 = c^2$(其中$a$、$b$为直角边,$c$为斜边),可得:
$BE=\sqrt{BD^{2}+DE^{2}}=\sqrt{3^{2}+3^{2}}=\sqrt{9 + 9}=\sqrt{18}=3\sqrt{2}$
【答案】:D
步骤一:根据中线的性质求出$BD$的长度
已知$AD$是$\triangle ABC$的中线,根据三角形中线的定义:三角形的中线是连接三角形顶点和它的对边中点的线段,可得$D$为$BC$中点。
因为$BC = 6$,所以$BD=\dfrac{1}{2}BC=\dfrac{1}{2}×6 = 3$。
步骤二:根据折叠的性质求出$DE$的长度以及$\angle EDA$的度数
由于$\triangle ADC$沿着直线$AD$对折,点$C$落在点$E$的位置,根据折叠的性质:折叠前后的图形全等,可得$\triangle ADE\cong\triangle ADC$。
所以$DE = DC$,$\angle EDA=\angle ADC = 45^{\circ}$。
又因为$D$为$BC$中点,$BC = 6$,所以$DC=\dfrac{1}{2}BC = 3$,则$DE = 3$。
步骤三:求出$\angle EDB$的度数
因为$\angle EDA = 45^{\circ}$,$\angle ADC = 45^{\circ}$,且$\angle EDA+\angle ADC+\angle EDB = 180^{\circ}$,所以$\angle EDB = 180^{\circ}-\angle EDA - \angle ADC = 180^{\circ}- 45^{\circ}- 45^{\circ}= 90^{\circ}$。
步骤四:在$Rt\triangle BDE$中利用勾股定理求出$BE$的长度
在$Rt\triangle BDE$中,$\angle EDB = 90^{\circ}$,$BD = 3$,$DE = 3$,根据勾股定理:在任何一个直角三角形中,两条直角边长的平方和等于斜边长的平方,即$a^2 + b^2 = c^2$(其中$a$、$b$为直角边,$c$为斜边),可得:
$BE=\sqrt{BD^{2}+DE^{2}}=\sqrt{3^{2}+3^{2}}=\sqrt{9 + 9}=\sqrt{18}=3\sqrt{2}$
【答案】:D
4. 如图,B,C,E 三点在同一条直线上,$AC= CD,∠B= ∠E= 90^{\circ },AB= CE$,则不正确的结论是 ( )
A.$∠A与∠D$互为余角
B.$∠A= ∠2$
C.$△ABC\cong △CED$
D.$∠1= ∠2$
A.$∠A与∠D$互为余角
B.$∠A= ∠2$
C.$△ABC\cong △CED$
D.$∠1= ∠2$
答案:
【解析】:
首先,我们根据题目条件,知道$B,C,E$三点在同一条直线上,且$AC= CD, ∠B= ∠E= 90^{\circ }, AB = CE$。
我们可以根据HL全等条件(直角三角形的斜边和一个直角边对应相等,则两直角三角形全等)来判断$\triangle ABC \cong \triangle CED$。
由于$AB = CE$,$AC = CD$,且$∠B = ∠E = 90^{\circ }$,所以根据HL全等条件,我们可以得出$\triangle ABC \cong \triangle CED$。
因此,选项C是正确的。
接下来,由于$\triangle ABC \cong \triangle CED$,根据全等三角形的性质,对应角相等,即$∠A = ∠2$。
因此,选项B也是正确的。
再根据全等三角形的性质,$∠A + ∠1 = 90^{\circ }$(因为$∠B = 90^{\circ }$,且$∠1$和$∠A$是$△ABC$中的两个锐角,它们的和加上$∠B$等于$180^{\circ }$),
同理$∠2 + ∠D = 90^{\circ }$。
由于$∠A = ∠2$,我们可以得出$∠A + ∠D = 90^{\circ }$,即$∠A$与$∠D$互为余角。
因此,选项A也是正确的。
最后,我们来看选项D,它说$∠1 = ∠2$。
但是,从我们的推理中,我们只能知道$∠A = ∠2$,并不能直接得出$∠1 = ∠2$。
实际上,$∠1$和$∠2$是两个不同的角,它们不一定相等。
因此,选项D是不正确的。
【答案】:D
首先,我们根据题目条件,知道$B,C,E$三点在同一条直线上,且$AC= CD, ∠B= ∠E= 90^{\circ }, AB = CE$。
我们可以根据HL全等条件(直角三角形的斜边和一个直角边对应相等,则两直角三角形全等)来判断$\triangle ABC \cong \triangle CED$。
由于$AB = CE$,$AC = CD$,且$∠B = ∠E = 90^{\circ }$,所以根据HL全等条件,我们可以得出$\triangle ABC \cong \triangle CED$。
因此,选项C是正确的。
接下来,由于$\triangle ABC \cong \triangle CED$,根据全等三角形的性质,对应角相等,即$∠A = ∠2$。
因此,选项B也是正确的。
再根据全等三角形的性质,$∠A + ∠1 = 90^{\circ }$(因为$∠B = 90^{\circ }$,且$∠1$和$∠A$是$△ABC$中的两个锐角,它们的和加上$∠B$等于$180^{\circ }$),
同理$∠2 + ∠D = 90^{\circ }$。
由于$∠A = ∠2$,我们可以得出$∠A + ∠D = 90^{\circ }$,即$∠A$与$∠D$互为余角。
因此,选项A也是正确的。
最后,我们来看选项D,它说$∠1 = ∠2$。
但是,从我们的推理中,我们只能知道$∠A = ∠2$,并不能直接得出$∠1 = ∠2$。
实际上,$∠1$和$∠2$是两个不同的角,它们不一定相等。
因此,选项D是不正确的。
【答案】:D
查看更多完整答案,请扫码查看


