5. 如图,OP是$∠AOC$的平分线,点B在OP上,$BD⊥OC$于D,$∠A= 45^{\circ }$.若$BD= 2$,则AB的长为 (
A.2
B.$2\sqrt {3}$
C.$2\sqrt {2}$
D.3
C
)A.2
B.$2\sqrt {3}$
C.$2\sqrt {2}$
D.3
答案:
【解析】:本题可先根据角平分线的性质求出$OB$到$OA$的距离,再通过构造直角三角形,利用勾股定理求出$AB$的长度。
过点$B$作$BE\perp OA$于点$E$。
因为$OP$是$\angle AOC$的平分线,$BD\perp OC$,$BE\perp OA$,根据角平分线的性质:角平分线上的点到角两边的距离相等,所以$BE = BD = 2$。
在$Rt\triangle ABE$中,$\angle A = 45^{\circ}$,则$\angle ABE = 180^{\circ}-90^{\circ}-45^{\circ}= 45^{\circ}$,所以$\triangle ABE$是等腰直角三角形,那么$AE = BE = 2$。
根据勾股定理$a^2+b^2=c^2$(其中$a$、$b$为直角边,$c$为斜边),在$Rt\triangle ABE$中,$AB=\sqrt{AE^{2}+BE^{2}}=\sqrt{2^{2} + 2^{2}}=\sqrt{4 + 4}=\sqrt{8}=2\sqrt{2}$。
【答案】:C
过点$B$作$BE\perp OA$于点$E$。
因为$OP$是$\angle AOC$的平分线,$BD\perp OC$,$BE\perp OA$,根据角平分线的性质:角平分线上的点到角两边的距离相等,所以$BE = BD = 2$。
在$Rt\triangle ABE$中,$\angle A = 45^{\circ}$,则$\angle ABE = 180^{\circ}-90^{\circ}-45^{\circ}= 45^{\circ}$,所以$\triangle ABE$是等腰直角三角形,那么$AE = BE = 2$。
根据勾股定理$a^2+b^2=c^2$(其中$a$、$b$为直角边,$c$为斜边),在$Rt\triangle ABE$中,$AB=\sqrt{AE^{2}+BE^{2}}=\sqrt{2^{2} + 2^{2}}=\sqrt{4 + 4}=\sqrt{8}=2\sqrt{2}$。
【答案】:C
6. 某风筝的骨架如图所示.为使风筝平衡,须使$∠AOP= ∠BOP$.已知$PC⊥OA,PD⊥OB$,那么PC和PD应满足
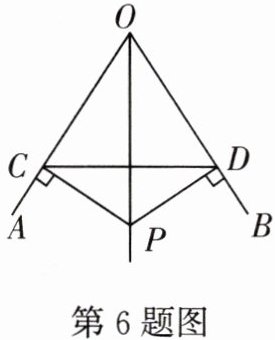
PC=PD
,才能保证OP为$∠AOB$的平分线.
答案:
解:PC=PD
证明:
∵PC⊥OA,PD⊥OB,
∴∠OCP=∠ODP=90°.
在Rt△OCP和Rt△ODP中,
∵OP=OP,PC=PD,
∴Rt△OCP≌Rt△ODP(HL).
∴∠AOP=∠BOP,即OP为∠AOB的平分线.
故PC和PD应满足PC=PD,才能保证OP为∠AOB的平分线.
证明:
∵PC⊥OA,PD⊥OB,
∴∠OCP=∠ODP=90°.
在Rt△OCP和Rt△ODP中,
∵OP=OP,PC=PD,
∴Rt△OCP≌Rt△ODP(HL).
∴∠AOP=∠BOP,即OP为∠AOB的平分线.
故PC和PD应满足PC=PD,才能保证OP为∠AOB的平分线.
7. 如图,在$△ABC$中,$AB= 4,AC= 3$,AD是$△ABC$的角平分线,则$△ABD与△ACD$的面积之比是
$4:3$
.
答案:
【解析】:本题可根据三角形面积公式,结合角平分线的性质来求解$\triangle ABD$与$\triangle ACD$的面积之比。
步骤一:明确三角形面积公式
三角形的面积公式为$S = \frac{1}{2}ah$(其中$S$表示三角形面积,$a$表示三角形的底边长,$h$表示这条底边对应的高)。
步骤二:找出$\triangle ABD$与$\triangle ACD$的底和高
已知$AD$是$\triangle ABC$的角平分线,根据角平分线的性质:角平分线上的点到角两边的距离相等,可知点$D$到$AB$的距离与点$D$到$AC$的距离相等,设这个距离为$h$。
对于$\triangle ABD$,底为$AB$,高为$h$,则其面积$S_{\triangle ABD}=\frac{1}{2}AB× h$;
对于$\triangle ACD$,底为$AC$,高为$h$,则其面积$S_{\triangle ACD}=\frac{1}{2}AC× h$。
步骤三:计算$\triangle ABD$与$\triangle ACD$的面积之比
将$S_{\triangle ABD}=\frac{1}{2}AB× h$,$S_{\triangle ACD}=\frac{1}{2}AC× h$代入$\frac{S_{\triangle ABD}}{S_{\triangle ACD}}$可得:
$\frac{S_{\triangle ABD}}{S_{\triangle ACD}}=\frac{\frac{1}{2}AB× h}{\frac{1}{2}AC× h}=\frac{AB}{AC}$
已知$AB = 4$,$AC = 3$,所以$\frac{AB}{AC}=\frac{4}{3}$,即$\triangle ABD$与$\triangle ACD$的面积之比是$4:3$。
【答案】:$4:3$
步骤一:明确三角形面积公式
三角形的面积公式为$S = \frac{1}{2}ah$(其中$S$表示三角形面积,$a$表示三角形的底边长,$h$表示这条底边对应的高)。
步骤二:找出$\triangle ABD$与$\triangle ACD$的底和高
已知$AD$是$\triangle ABC$的角平分线,根据角平分线的性质:角平分线上的点到角两边的距离相等,可知点$D$到$AB$的距离与点$D$到$AC$的距离相等,设这个距离为$h$。
对于$\triangle ABD$,底为$AB$,高为$h$,则其面积$S_{\triangle ABD}=\frac{1}{2}AB× h$;
对于$\triangle ACD$,底为$AC$,高为$h$,则其面积$S_{\triangle ACD}=\frac{1}{2}AC× h$。
步骤三:计算$\triangle ABD$与$\triangle ACD$的面积之比
将$S_{\triangle ABD}=\frac{1}{2}AB× h$,$S_{\triangle ACD}=\frac{1}{2}AC× h$代入$\frac{S_{\triangle ABD}}{S_{\triangle ACD}}$可得:
$\frac{S_{\triangle ABD}}{S_{\triangle ACD}}=\frac{\frac{1}{2}AB× h}{\frac{1}{2}AC× h}=\frac{AB}{AC}$
已知$AB = 4$,$AC = 3$,所以$\frac{AB}{AC}=\frac{4}{3}$,即$\triangle ABD$与$\triangle ACD$的面积之比是$4:3$。
【答案】:$4:3$
8. 如图,在$△ABC$中,$∠ABC= 90^{\circ }$,BD为AC边的中线,过点C作$CE// AB$与BD的延长线交于点E.求证:$∠A= ∠E.$
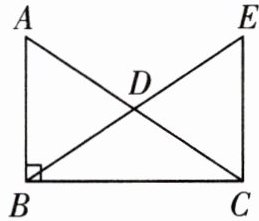

答案:
【解析】:本题主要考查了平行线的性质,以及直角三角形斜边上的中线性质。
先根据直角三角形斜边上的中线性质得到$BD=AD=DC$,由等边对等角得到$\angle A=\angle ABD$,再根据平行线的性质得到$\angle ABD=\angle E$,通过等量代换即可证明$\angle A=\angle E$。
【答案】:证明:
∵$∠ABC=90^{\circ}$,BD为AC边的中线,
∴$BD=AD=DC$,
∴$\angle A=\angle ABD$,
∵$CE// AB$,
∴$\angle ABD=\angle E$,
∴$\angle A=\angle E$。
先根据直角三角形斜边上的中线性质得到$BD=AD=DC$,由等边对等角得到$\angle A=\angle ABD$,再根据平行线的性质得到$\angle ABD=\angle E$,通过等量代换即可证明$\angle A=\angle E$。
【答案】:证明:
∵$∠ABC=90^{\circ}$,BD为AC边的中线,
∴$BD=AD=DC$,
∴$\angle A=\angle ABD$,
∵$CE// AB$,
∴$\angle ABD=\angle E$,
∴$\angle A=\angle E$。
9. 如图,已知$PA⊥ON$于点A,$PB⊥OM$于点B,且$PA= PB,∠MON= 50^{\circ },∠OPC= 30^{\circ }$,求$∠PCA$的大小.
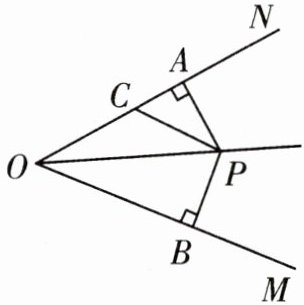

答案:
解:
∵PA⊥ON,PB⊥OM,PA=PB,
∴OP平分∠MON(角平分线的判定定理).
∵∠MON=50°,
∴∠AOP=∠BOP=25°.
在Rt△OAP中,∠PAO=90°,
∴∠OPA=90°-∠AOP=90°-25°=65°.
∵∠OPC=30°,
∴∠APC=∠OPA-∠OPC=65°-30°=35°.
∵PA⊥ON,
∴∠PAC=90°,
∴∠PCA=90°-∠APC=90°-35°=55°.
答:∠PCA的大小为55°.
∵PA⊥ON,PB⊥OM,PA=PB,
∴OP平分∠MON(角平分线的判定定理).
∵∠MON=50°,
∴∠AOP=∠BOP=25°.
在Rt△OAP中,∠PAO=90°,
∴∠OPA=90°-∠AOP=90°-25°=65°.
∵∠OPC=30°,
∴∠APC=∠OPA-∠OPC=65°-30°=35°.
∵PA⊥ON,
∴∠PAC=90°,
∴∠PCA=90°-∠APC=90°-35°=55°.
答:∠PCA的大小为55°.
查看更多完整答案,请扫码查看


