5.平行四边形的内角平分线能够围成的四边形是 (
A.梯形
B.矩形
C.正方形
D.不是平行四边形
B
)A.梯形
B.矩形
C.正方形
D.不是平行四边形
答案:
【解析】:
本题主要考查平行四边形的性质以及矩形判定。
首先,由平行四边形的性质,我们知道其相对的两个角是互补的,即$\angle A + \angle B = 180^\circ$。
设平行四边形的一个角为$\angle A$,其邻角为$\angle B$,那么有$\angle A + \angle B = 180^\circ$。
当我们将$\angle A$和$\angle B$都平分,得到两个角$\angle 1$和$\angle 2$,由于$\angle A + \angle B = 180^\circ$,那么$\angle 1 + \angle 2 = \frac{1}{2}(\angle A + \angle B) = 90^\circ$。
这意味着新形成的四边形在每个角都是$90^\circ$,即该四边形是一个矩形。
接下来,我们根据矩形的性质进行推理:
矩形的定义是四个内角均为直角的四边形。
在新形成的四边形中,由于每个角都是由平行四边形的两个内角的平分线相交形成的,且每个角都是$90^\circ$,因此这个四边形满足矩形的定义。
最后,我们根据选项进行判定:
A. 梯形:梯形只有一对平行的边,而新形成的四边形每个角都是直角,不可能是梯形。
B. 矩形:新形成的四边形每个角都是直角,符合矩形的定义。
C. 正方形:正方形是矩形的一个特例,其中所有的边都相等。题目没有给出足够的信息来证明新形成的四边形是正方形。
D. 不是平行四边形:新形成的四边形每个角都是直角,显然是平行四边形(实际上是矩形)。
【答案】:B. 矩形。
本题主要考查平行四边形的性质以及矩形判定。
首先,由平行四边形的性质,我们知道其相对的两个角是互补的,即$\angle A + \angle B = 180^\circ$。
设平行四边形的一个角为$\angle A$,其邻角为$\angle B$,那么有$\angle A + \angle B = 180^\circ$。
当我们将$\angle A$和$\angle B$都平分,得到两个角$\angle 1$和$\angle 2$,由于$\angle A + \angle B = 180^\circ$,那么$\angle 1 + \angle 2 = \frac{1}{2}(\angle A + \angle B) = 90^\circ$。
这意味着新形成的四边形在每个角都是$90^\circ$,即该四边形是一个矩形。
接下来,我们根据矩形的性质进行推理:
矩形的定义是四个内角均为直角的四边形。
在新形成的四边形中,由于每个角都是由平行四边形的两个内角的平分线相交形成的,且每个角都是$90^\circ$,因此这个四边形满足矩形的定义。
最后,我们根据选项进行判定:
A. 梯形:梯形只有一对平行的边,而新形成的四边形每个角都是直角,不可能是梯形。
B. 矩形:新形成的四边形每个角都是直角,符合矩形的定义。
C. 正方形:正方形是矩形的一个特例,其中所有的边都相等。题目没有给出足够的信息来证明新形成的四边形是正方形。
D. 不是平行四边形:新形成的四边形每个角都是直角,显然是平行四边形(实际上是矩形)。
【答案】:B. 矩形。
6.如图,MN//PQ,AB⊥PQ,点A,D,B,C分别在直线MN和PQ上,点E在AB上,AD+BC= 7,AD= EB,DE= EC,则AB的长为
7
.
答案:
【解析】:本题考查全等三角形的判定和性质。
由于$MN// PQ$,$AB\perp PQ$,
我们可以得到$AD// BE$,$\angle DAE=\angle EBC=90^\circ$。
因为$AD=BE$,$DE=EC$,且$\angle DAE=\angle EBC$,
根据$HL$全等条件,我们可以得出$\triangle ADE\cong \triangle BEC$($HL$)。
由全等三角形的性质,我们知道对应边相等,所以$AE=BC$。
根据题目给出的$AD+BC=7$,且$AD=BE$,
我们可以得出$AE+BE=7$,即$AB=AE+BE=7$。
【答案】:$AB=7$。
由于$MN// PQ$,$AB\perp PQ$,
我们可以得到$AD// BE$,$\angle DAE=\angle EBC=90^\circ$。
因为$AD=BE$,$DE=EC$,且$\angle DAE=\angle EBC$,
根据$HL$全等条件,我们可以得出$\triangle ADE\cong \triangle BEC$($HL$)。
由全等三角形的性质,我们知道对应边相等,所以$AE=BC$。
根据题目给出的$AD+BC=7$,且$AD=BE$,
我们可以得出$AE+BE=7$,即$AB=AE+BE=7$。
【答案】:$AB=7$。
7.用若干个全等的正五边形可以拼成一个环状,前3个正五边形的拼接情况如图.要完全拼成一个圆环还需要正五边形
2
个.
答案:
解:正五边形每个内角为$\frac{(5-2)×180^\circ}{5}=108^\circ$。
拼接时,每个拼接点处由两个正五边形的内角和一个圆心角组成,圆心角为$360^\circ - 2×108^\circ = 144^\circ$。
圆环一周圆心角总和为$360^\circ$,所需正五边形个数为$\frac{360^\circ}{144^\circ}=5$。
已拼接3个,还需$5 - 3 = 2$个。
2
拼接时,每个拼接点处由两个正五边形的内角和一个圆心角组成,圆心角为$360^\circ - 2×108^\circ = 144^\circ$。
圆环一周圆心角总和为$360^\circ$,所需正五边形个数为$\frac{360^\circ}{144^\circ}=5$。
已拼接3个,还需$5 - 3 = 2$个。
2
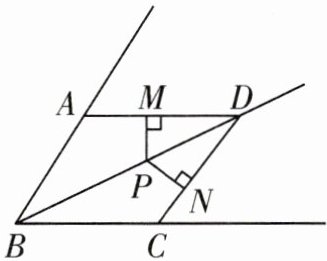
8.如图,已知BD为∠ABC的平分线,AB= BC,点P在BD上,PM⊥AD于M,PN⊥CD于N.求证:PM= PN.

答案:
【解析】:本题主要考查了角平分线的性质以及全等三角形的判定与性质。
首先,根据题目条件“$BD$为$\angle ABC$的平分线”和“$AB = BC$”,可以利用$SAS$(边角边)全等条件证明$\triangle ABD$与$\triangle CBD$全等。
由于$\triangle ABD \cong \triangle CBD$,根据全等三角形的对应角相等,得出$\angle ADB = \angle CDB$,即$BD$平分$\angle ADC$。
接着,根据角平分线的性质,即角平分线上的点到这个角的两边的距离相等,由于点$P$在$BD$上,且$PM \perp AD$,$PN \perp CD$,可以得出$PM = PN$。
【答案】:证明:
∵$BD$为$\angle ABC$的平分线,
∴$\angle ABD=\angle CBD$,
在$\triangle ABD$和$\triangle CBD$中,
$\left\{\begin{matrix}AB=BC,\\\angle ABD=\angle CBD,\\BD=BD.\end{matrix}\right.$
∴$\triangle ABD\cong \triangle CBD(SAS)$,
∴$\angle ADB=\angle CDB$,
即$BD$平分$\angle ADC$,
∵$PM\perp AD$,$PN\perp CD$,
∴$PM=PN$。
首先,根据题目条件“$BD$为$\angle ABC$的平分线”和“$AB = BC$”,可以利用$SAS$(边角边)全等条件证明$\triangle ABD$与$\triangle CBD$全等。
由于$\triangle ABD \cong \triangle CBD$,根据全等三角形的对应角相等,得出$\angle ADB = \angle CDB$,即$BD$平分$\angle ADC$。
接着,根据角平分线的性质,即角平分线上的点到这个角的两边的距离相等,由于点$P$在$BD$上,且$PM \perp AD$,$PN \perp CD$,可以得出$PM = PN$。
【答案】:证明:
∵$BD$为$\angle ABC$的平分线,
∴$\angle ABD=\angle CBD$,
在$\triangle ABD$和$\triangle CBD$中,
$\left\{\begin{matrix}AB=BC,\\\angle ABD=\angle CBD,\\BD=BD.\end{matrix}\right.$
∴$\triangle ABD\cong \triangle CBD(SAS)$,
∴$\angle ADB=\angle CDB$,
即$BD$平分$\angle ADC$,
∵$PM\perp AD$,$PN\perp CD$,
∴$PM=PN$。
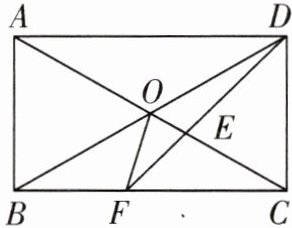
9.如图,在矩形ABCD中,∠ADC的平分线DF交AC于点E,交BC于点F,∠BDF= 15°,求∠DOC和∠COF的度数.

答案:
解:
∵四边形ABCD是矩形,
∴∠ADC=90°,OD=OC,AC=BD,OA=OC=OB=OD(矩形对角线相等且互相平分),
∴△ODC是等腰三角形。
∵DF平分∠ADC,
∴∠CDF=∠ADC/2=45°。
∵∠BDF=15°,
∴∠ODC=∠CDF+∠BDF=45°+15°=60°。
∵OD=OC,∠ODC=60°,
∴△ODC是等边三角形,
∴∠DOC=60°,OC=CD。
在Rt△DCF中,∠CDF=45°,
∴∠CFD=45°,
∴CF=CD(等角对等边)。
∵OC=CD,CF=CD,
∴OC=CF,
∴△OCF是等腰三角形。
∵∠OCD=60°(等边三角形内角),∠BCD=90°(矩形内角),
∴∠OCF=∠BCD-∠OCD=90°-60°=30°。
∴∠COF=(180°-∠OCF)/2=(180°-30°)/2=75°。
综上,∠DOC=60°,∠COF=75°。
∵四边形ABCD是矩形,
∴∠ADC=90°,OD=OC,AC=BD,OA=OC=OB=OD(矩形对角线相等且互相平分),
∴△ODC是等腰三角形。
∵DF平分∠ADC,
∴∠CDF=∠ADC/2=45°。
∵∠BDF=15°,
∴∠ODC=∠CDF+∠BDF=45°+15°=60°。
∵OD=OC,∠ODC=60°,
∴△ODC是等边三角形,
∴∠DOC=60°,OC=CD。
在Rt△DCF中,∠CDF=45°,
∴∠CFD=45°,
∴CF=CD(等角对等边)。
∵OC=CD,CF=CD,
∴OC=CF,
∴△OCF是等腰三角形。
∵∠OCD=60°(等边三角形内角),∠BCD=90°(矩形内角),
∴∠OCF=∠BCD-∠OCD=90°-60°=30°。
∴∠COF=(180°-∠OCF)/2=(180°-30°)/2=75°。
综上,∠DOC=60°,∠COF=75°。
查看更多完整答案,请扫码查看


