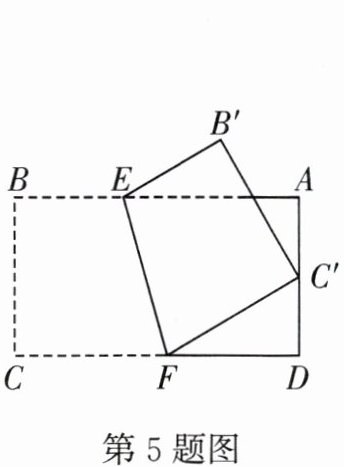
5.如图,将矩形纸片ABCD沿直线EF翻折,使点C落在AD边的中点$C'$处,点B落在点$B'$处,其中$AB= 9,BC= 6$,则$FC'$的长为 (
A.$\frac {10}{3}$
B.4
C.4.5
D.5
D
)
A.$\frac {10}{3}$
B.4
C.4.5
D.5
答案:
【解析】:本题主要考查矩形的性质、折叠的性质以及勾股定理。
设$FC' = x$,由于折叠的性质可知$FC = FC' = x$,那么$FD = 9 - x$。
因为点$C'$是$AD$边的中点,$AD = BC = 6$,所以$C'D = 3$。
在$Rt\triangle FDC'$中,根据勾股定理$a^2 + b^2 = c^2$(其中$a$、$b$为直角边,$c$为斜边),可得$FC'^{2}=FD^{2}+C'D^{2}$,即$x^{2}=(9 - x)^{2}+3^{2}$。
接下来求解上述方程:
$\begin{aligned}x^{2}&=(9 - x)^{2}+3^{2}\\x^{2}&=81 - 18x + x^{2}+9\\18x&=81 + 9\\18x&=90\\x&= 5\end{aligned}$
所以$FC'$的长为$5$。
【答案】:D。
设$FC' = x$,由于折叠的性质可知$FC = FC' = x$,那么$FD = 9 - x$。
因为点$C'$是$AD$边的中点,$AD = BC = 6$,所以$C'D = 3$。
在$Rt\triangle FDC'$中,根据勾股定理$a^2 + b^2 = c^2$(其中$a$、$b$为直角边,$c$为斜边),可得$FC'^{2}=FD^{2}+C'D^{2}$,即$x^{2}=(9 - x)^{2}+3^{2}$。
接下来求解上述方程:
$\begin{aligned}x^{2}&=(9 - x)^{2}+3^{2}\\x^{2}&=81 - 18x + x^{2}+9\\18x&=81 + 9\\18x&=90\\x&= 5\end{aligned}$
所以$FC'$的长为$5$。
【答案】:D。
6.如图,在$Rt△ABC$中,$∠ABC= 90^{\circ }$,D为AC的中点,若$∠C= 55^{\circ }$,则$∠ABD$的度数为
$35^{\circ}$
.
答案:
【解析】:本题可根据直角三角形的性质求出$\angle BAC$的度数,再结合中点的性质得到$BD$与$AC$的关系,进而求出$\angle ABD$的度数。
步骤一:求$\angle BAC$的度数
在$Rt\triangle ABC$中,已知$\angle ABC = 90^{\circ}$,$\angle C = 55^{\circ}$,根据三角形内角和为$180^{\circ}$,可得:
$\angle BAC=180^{\circ}-\angle ABC - \angle C=180^{\circ}-90^{\circ}-55^{\circ}=35^{\circ}$
步骤二:分析$BD$与$AC$的关系
因为$D$为$AC$的中点,在直角三角形中,斜边上的中线等于斜边的一半,所以在$Rt\triangle ABC$中,$BD$是斜边$AC$上的中线,则有$BD = \frac{1}{2}AC = AD = CD$。
步骤三:求$\angle ABD$的度数
由于$BD = AD$,根据等腰三角形的性质:等腰三角形的两个底角相等,所以$\angle ABD = \angle BAC = 35^{\circ}$。
【答案】:$35^{\circ}$
步骤一:求$\angle BAC$的度数
在$Rt\triangle ABC$中,已知$\angle ABC = 90^{\circ}$,$\angle C = 55^{\circ}$,根据三角形内角和为$180^{\circ}$,可得:
$\angle BAC=180^{\circ}-\angle ABC - \angle C=180^{\circ}-90^{\circ}-55^{\circ}=35^{\circ}$
步骤二:分析$BD$与$AC$的关系
因为$D$为$AC$的中点,在直角三角形中,斜边上的中线等于斜边的一半,所以在$Rt\triangle ABC$中,$BD$是斜边$AC$上的中线,则有$BD = \frac{1}{2}AC = AD = CD$。
步骤三:求$\angle ABD$的度数
由于$BD = AD$,根据等腰三角形的性质:等腰三角形的两个底角相等,所以$\angle ABD = \angle BAC = 35^{\circ}$。
【答案】:$35^{\circ}$
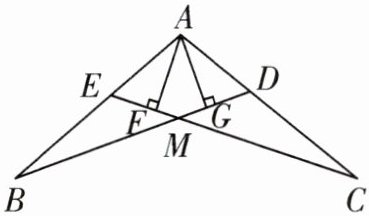
7.如图,$AB= AC$,点D,E分别在AC,AB上,$AG⊥BD$,垂足为点G,$AF⊥CE$,垂足为点F,且$AE= AD,EF= DG$.求证:$BG= CF$.

答案:
证明:
∵AG⊥BD,AF⊥CE,
∴∠AFE=∠AGD=90°。
在Rt△AFE和Rt△AGD中,
$\left\{\begin{array}{l} AE=AD,\\ EF=DG,\end{array}\right.$
∴Rt△AFE≌Rt△AGD(HL),
∴AF=AG。
∵AB=AC,AE=AD,
∴AB-AE=AC-AD,即BE=CD。
在Rt△AFB和Rt△AGC中,
$\left\{\begin{array}{l} AB=AC,\\ AF=AG,\end{array}\right.$
∴Rt△AFB≌Rt△AGC(HL),
∴BF=CG。
∵BF=BE+EF,CG=CD+DG,且BE=CD,EF=DG,
∴BF=CG,
∴BF-EF=CG-DG,即BG=CF。
结论:BG=CF。
∵AG⊥BD,AF⊥CE,
∴∠AFE=∠AGD=90°。
在Rt△AFE和Rt△AGD中,
$\left\{\begin{array}{l} AE=AD,\\ EF=DG,\end{array}\right.$
∴Rt△AFE≌Rt△AGD(HL),
∴AF=AG。
∵AB=AC,AE=AD,
∴AB-AE=AC-AD,即BE=CD。
在Rt△AFB和Rt△AGC中,
$\left\{\begin{array}{l} AB=AC,\\ AF=AG,\end{array}\right.$
∴Rt△AFB≌Rt△AGC(HL),
∴BF=CG。
∵BF=BE+EF,CG=CD+DG,且BE=CD,EF=DG,
∴BF=CG,
∴BF-EF=CG-DG,即BG=CF。
结论:BG=CF。
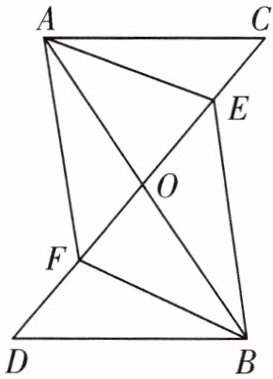
8.如图,AB,CD相交于点O,$AC// DB,AO= BO$,E,F分别是OC,OD的中点.求证:四边形AFBE是平行四边形.

答案:
【解析】:本题主要考查平行四边形的判定,全等三角形的性质和判定以及平行线的性质。首先,根据平行线的性质,得到两对角相等,再加上一组对边相等($AO = BO$),利用$AAS$(角角边)判定$\triangle AOC$和$\triangle BOD$全等,从而得到$AC = BD$,$OC = OD$。然后,利用中点的性质,得到$OE = OF$。最后,根据平行四边形的判定条件(两组对边分别相等的四边形是平行四边形),证明四边形$AFBE$是平行四边形。
【答案】:
证明:
∵$AC// DB$,
∴$\angle C = \angle D$,$\angle CAO = \angle DBO$(两直线平行,内错角相等)。
在$\triangle AOC$和$\triangle BOD$中,
$\left\{\begin{matrix}\angle C = \angle D,\\\angle CAO = \angle DBO,\\AO = BO.\end{matrix}\right.$
∴$\triangle AOC\cong\triangle BOD$($AAS$)。
∴$AC = BD$,$OC = OD$(全等三角形的对应边相等)。
∵$E$,$F$分别是$OC$,$OD$的中点,
∴$OE=\frac{1}{2}OC$,$OF=\frac{1}{2}OD$(中点的定义)。
∴$OE = OF$。
又
∵$AO = BO$,
∴四边形$AFBE$是平行四边形(两组对边分别相等的四边形是平行四边形)。
【答案】:
证明:
∵$AC// DB$,
∴$\angle C = \angle D$,$\angle CAO = \angle DBO$(两直线平行,内错角相等)。
在$\triangle AOC$和$\triangle BOD$中,
$\left\{\begin{matrix}\angle C = \angle D,\\\angle CAO = \angle DBO,\\AO = BO.\end{matrix}\right.$
∴$\triangle AOC\cong\triangle BOD$($AAS$)。
∴$AC = BD$,$OC = OD$(全等三角形的对应边相等)。
∵$E$,$F$分别是$OC$,$OD$的中点,
∴$OE=\frac{1}{2}OC$,$OF=\frac{1}{2}OD$(中点的定义)。
∴$OE = OF$。
又
∵$AO = BO$,
∴四边形$AFBE$是平行四边形(两组对边分别相等的四边形是平行四边形)。
查看更多完整答案,请扫码查看


