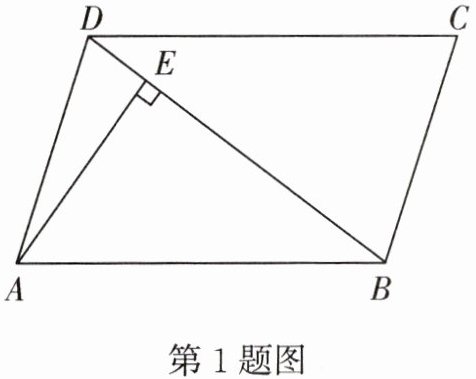
1.如图,在$□ ABCD$中,$DB= DC,∠C= 70^{\circ },AE⊥BD$于E,则$∠DAE$等于 (
A.$35^{\circ }$
B.$30^{\circ }$
C.$25^{\circ }$
D.$20^{\circ }$
D
)
A.$35^{\circ }$
B.$30^{\circ }$
C.$25^{\circ }$
D.$20^{\circ }$
答案:
解:
∵四边形ABCD是平行四边形,
∴AD//BC,∠ADC + ∠C = 180°,∠ADB = ∠DBC。
∵∠C = 70°,
∴∠ADC = 180° - 70° = 110°。
∵DB = DC,
∴∠DBC = ∠C = 70°,
∴∠ADB = ∠DBC = 70°。
∵AE⊥BD,
∴∠AED = 90°,
∴∠DAE = 90° - ∠ADB = 90° - 70° = 20°。
答案:D
∵四边形ABCD是平行四边形,
∴AD//BC,∠ADC + ∠C = 180°,∠ADB = ∠DBC。
∵∠C = 70°,
∴∠ADC = 180° - 70° = 110°。
∵DB = DC,
∴∠DBC = ∠C = 70°,
∴∠ADB = ∠DBC = 70°。
∵AE⊥BD,
∴∠AED = 90°,
∴∠DAE = 90° - ∠ADB = 90° - 70° = 20°。
答案:D
2.如图,点E在正方形ABCD内,满足$∠AEB= 90^{\circ },AE= 6,BE= 8$,则阴影部分的面积是 (
A.48
B.60
C.76
D.80
C
)A.48
B.60
C.76
D.80
答案:
【解析】:本题主要考察勾股定理以及正方形面积的计算。
由题可知,$\bigtriangleup AEB$为直角三角形,根据勾股定理可求出$AB$的长度,又因为$ABCD$为正方形,即可求出正方形$ABCD$的面积,通过$S_{阴影}=S_{正方形ABCD}-S_{\bigtriangleup AEB}$可求出阴影部分的面积。
在直角三角形$AEB$中,根据勾股定理,有:
$AB^2 = AE^2 + BE^2$,
代入已知条件 $AE = 6, BE = 8$,得:
$AB^2 = 6^2 + 8^2 = 36 + 64 = 100$,
所以,$AB = \sqrt{100} = 10$,
由于$ABCD$是正方形,所以其面积为:
$S_{正方形ABCD} = AB^2 = 10^2 = 100$,
直角三角形$AEB$的面积为:
$S_{\bigtriangleup AEB} = \frac{1}{2} × AE × BE = \frac{1}{2} × 6 × 8 = 24$,
阴影部分的面积为:
$S_{阴影} = S_{正方形ABCD} - S_{\bigtriangleup AEB} = 100 - 24 = 76$。
【答案】:C
由题可知,$\bigtriangleup AEB$为直角三角形,根据勾股定理可求出$AB$的长度,又因为$ABCD$为正方形,即可求出正方形$ABCD$的面积,通过$S_{阴影}=S_{正方形ABCD}-S_{\bigtriangleup AEB}$可求出阴影部分的面积。
在直角三角形$AEB$中,根据勾股定理,有:
$AB^2 = AE^2 + BE^2$,
代入已知条件 $AE = 6, BE = 8$,得:
$AB^2 = 6^2 + 8^2 = 36 + 64 = 100$,
所以,$AB = \sqrt{100} = 10$,
由于$ABCD$是正方形,所以其面积为:
$S_{正方形ABCD} = AB^2 = 10^2 = 100$,
直角三角形$AEB$的面积为:
$S_{\bigtriangleup AEB} = \frac{1}{2} × AE × BE = \frac{1}{2} × 6 × 8 = 24$,
阴影部分的面积为:
$S_{阴影} = S_{正方形ABCD} - S_{\bigtriangleup AEB} = 100 - 24 = 76$。
【答案】:C
3.如图,在$△ABC$中,$∠C= 90^{\circ },ED⊥AB$于点D,$BD= BC$.若$AC= 6cm$,则$AE+DE$等于 (
A.4 cm
B.5 cm
C.6 cm
D.7 cm
C
)A.4 cm
B.5 cm
C.6 cm
D.7 cm
答案:
【解析】:本题可根据角平分线的性质以及全等三角形的判定和性质来求解$AE + DE$的值。
步骤一:证明$\triangle BDE\cong\triangle BCE$
已知$ED\perp AB$,$\angle C = 90^{\circ}$,所以$\angle BDE=\angle C = 90^{\circ}$。
在$Rt\triangle BDE$和$Rt\triangle BCE$中,$BD = BC$(已知),$BE$为公共边。
根据“斜边和一条直角边对应相等的两个直角三角形全等”($HL$定理),可得$Rt\triangle BDE\cong Rt\triangle BCE$。
步骤二:根据全等三角形的性质得到$DE = CE$
因为$\triangle BDE\cong\triangle BCE$,根据全等三角形的对应边相等,所以$DE = CE$。
步骤三:计算$AE + DE$的值
将$DE = CE$代入$AE + DE$中,可得$AE + DE = AE + CE$。
而$AE + CE = AC$,已知$AC = 6cm$,所以$AE + DE = 6cm$。
【答案】:C
步骤一:证明$\triangle BDE\cong\triangle BCE$
已知$ED\perp AB$,$\angle C = 90^{\circ}$,所以$\angle BDE=\angle C = 90^{\circ}$。
在$Rt\triangle BDE$和$Rt\triangle BCE$中,$BD = BC$(已知),$BE$为公共边。
根据“斜边和一条直角边对应相等的两个直角三角形全等”($HL$定理),可得$Rt\triangle BDE\cong Rt\triangle BCE$。
步骤二:根据全等三角形的性质得到$DE = CE$
因为$\triangle BDE\cong\triangle BCE$,根据全等三角形的对应边相等,所以$DE = CE$。
步骤三:计算$AE + DE$的值
将$DE = CE$代入$AE + DE$中,可得$AE + DE = AE + CE$。
而$AE + CE = AC$,已知$AC = 6cm$,所以$AE + DE = 6cm$。
【答案】:C
4.在四边形ABCD中,$∠A+∠B+∠C+∠D= 360^{\circ },∠A= ∠C,∠B= ∠D,AB= 5$,则CD的长为 (
A.20
B.10
C.5
D.2.5
C
)A.20
B.10
C.5
D.2.5
答案:
【解析】:
本题主要考查四边形的内角和性质以及等腰四边形的性质。
根据四边形的内角和性质,有:
$\angle A + \angle B + \angle C + \angle D = 360^{\circ}$
由题意知,$\angle A = \angle C$ 且 $\angle B = \angle D$。
将这两个条件代入四边形的内角和公式中,得到:
$2\angle A + 2\angle B = 360^{\circ}$
$\Rightarrow \angle A + \angle B = 180^{\circ}$
由于$\angle A$ 和 $\angle B$ 互补,且$\angle A = \angle C$,$\angle B = \angle D$,可以推断出四边形ABCD的两组对角都是互补的,即AB与CD平行,且AD与BC平行(同旁内角互补,两直线平行)。但这并不直接说明ABCD是矩形或正方形,仅说明它是一个等腰四边形,且两组对边分别平行,即ABCD是一个平行四边形。
在平行四边形中,对边相等,即:
$AB = CD$
由题意知,$AB = 5$,所以:
$CD = 5$
【答案】:
C. $5$
本题主要考查四边形的内角和性质以及等腰四边形的性质。
根据四边形的内角和性质,有:
$\angle A + \angle B + \angle C + \angle D = 360^{\circ}$
由题意知,$\angle A = \angle C$ 且 $\angle B = \angle D$。
将这两个条件代入四边形的内角和公式中,得到:
$2\angle A + 2\angle B = 360^{\circ}$
$\Rightarrow \angle A + \angle B = 180^{\circ}$
由于$\angle A$ 和 $\angle B$ 互补,且$\angle A = \angle C$,$\angle B = \angle D$,可以推断出四边形ABCD的两组对角都是互补的,即AB与CD平行,且AD与BC平行(同旁内角互补,两直线平行)。但这并不直接说明ABCD是矩形或正方形,仅说明它是一个等腰四边形,且两组对边分别平行,即ABCD是一个平行四边形。
在平行四边形中,对边相等,即:
$AB = CD$
由题意知,$AB = 5$,所以:
$CD = 5$
【答案】:
C. $5$
查看更多完整答案,请扫码查看


