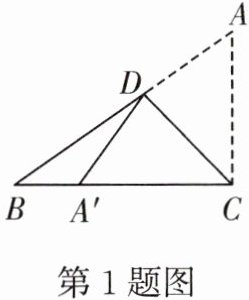
1. 如图,在$Rt△ABC$中,$∠ACB= 90^{\circ },∠A= 55^{\circ }$,将其折叠,使点A落在边CB上的点$A'$处,折痕为CD,则$∠A'DB$的度数为 ( )
A.$40^{\circ }$
B.$30^{\circ }$
C.$20^{\circ }$
D.$10^{\circ }$

A.$40^{\circ }$
B.$30^{\circ }$
C.$20^{\circ }$
D.$10^{\circ }$
答案:
【解析】:本题主要考查了图形的翻折变换以及三角形内角和定理。
在$Rt\bigtriangleup ABC$中,$\angle ACB = 90^{\circ}$,$\angle A = 55^{\circ}$,
根据三角形内角和为$180^{\circ}$,可得$\angle B = 180^{\circ} - 90^{\circ} - 55^{\circ} = 35^{\circ}$。
因为将$\bigtriangleup ABC$折叠,使点$A$落在边$CB$上的点$A'$处,折痕为$CD$,
所以$\angle CA'D = \angle A = 55^{\circ}$(翻折前后对应角相等)。
在$\bigtriangleup A'DB$中,$\angle CA'D$是$\bigtriangleup A'DB$的一个外角,
根据三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和,
可得$\angle A'DB = \angle CA'D - \angle B = 55^{\circ} - 35^{\circ} = 20^{\circ}$。
【答案】:C
在$Rt\bigtriangleup ABC$中,$\angle ACB = 90^{\circ}$,$\angle A = 55^{\circ}$,
根据三角形内角和为$180^{\circ}$,可得$\angle B = 180^{\circ} - 90^{\circ} - 55^{\circ} = 35^{\circ}$。
因为将$\bigtriangleup ABC$折叠,使点$A$落在边$CB$上的点$A'$处,折痕为$CD$,
所以$\angle CA'D = \angle A = 55^{\circ}$(翻折前后对应角相等)。
在$\bigtriangleup A'DB$中,$\angle CA'D$是$\bigtriangleup A'DB$的一个外角,
根据三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和,
可得$\angle A'DB = \angle CA'D - \angle B = 55^{\circ} - 35^{\circ} = 20^{\circ}$。
【答案】:C
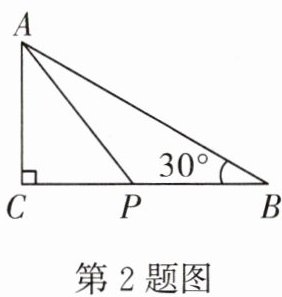
2. 如图,在$△ABC$中,$∠C= 90^{\circ },AC= 3,∠B= 30^{\circ }$,P是BC边上的动点,则AP的长不可能是 (
A.3.5
B.4.2
C.5.6
D.7
D
)
A.3.5
B.4.2
C.5.6
D.7
答案:
【解析】:本题可根据直角三角形的性质求出$AB$的取值范围,再结合垂线段最短的性质确定$AP$的取值范围,进而判断$AP$的长不可能是哪个选项。
在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$,$AC = 3$。
根据在直角三角形中,$30^{\circ}$所对的直角边等于斜边的一半,可得$AB = 2AC = 2×3 = 6$。
因为垂线段最短,当$AP\perp BC$时,$AP$最短,此时$AP = AC = 3$(直角三角形斜边上的高把斜边分成的两条线段与直角边构成的两个小直角三角形与原三角形相似,可得$AP = AC = 3$ )。
又因为$P$是$BC$边上的动点,所以$AP$的取值范围是$3\leqslant AP\leqslant 6$。
逐一分析选项:
选项A:$3\lt 3.5\lt 6$,$3.5$在$AP$的取值范围内,该选项不符合题意。
选项B:$3\lt 4.2\lt 6$,$4.2$在$AP$的取值范围内,该选项不符合题意。
选项C:$3\lt 5.6\lt 6$,$5.6$在$AP$的取值范围内,该选项不符合题意。
选项D:$7\gt 6$,$7$不在$AP$的取值范围内,该选项符合题意。
【答案】:D
在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$,$AC = 3$。
根据在直角三角形中,$30^{\circ}$所对的直角边等于斜边的一半,可得$AB = 2AC = 2×3 = 6$。
因为垂线段最短,当$AP\perp BC$时,$AP$最短,此时$AP = AC = 3$(直角三角形斜边上的高把斜边分成的两条线段与直角边构成的两个小直角三角形与原三角形相似,可得$AP = AC = 3$ )。
又因为$P$是$BC$边上的动点,所以$AP$的取值范围是$3\leqslant AP\leqslant 6$。
逐一分析选项:
选项A:$3\lt 3.5\lt 6$,$3.5$在$AP$的取值范围内,该选项不符合题意。
选项B:$3\lt 4.2\lt 6$,$4.2$在$AP$的取值范围内,该选项不符合题意。
选项C:$3\lt 5.6\lt 6$,$5.6$在$AP$的取值范围内,该选项不符合题意。
选项D:$7\gt 6$,$7$不在$AP$的取值范围内,该选项符合题意。
【答案】:D
3. 如图,分别以三角形的三边为直径向外作三个半圆,如果较小的两个半圆的面积之和等于最大的半圆的面积,那么这个三角形为 (

A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定形状
B
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定形状
答案:
【解析】:本题可根据圆的面积公式分别表示出三个半圆的面积,再结合已知条件“较小的两个半圆的面积之和等于最大的半圆的面积”列出等式,最后根据勾股定理的逆定理判断三角形的形状。
设三个半圆的直径分别为$a$、$b$、$c$($c$为最大半圆的直径),根据圆的面积公式$S = \pi r^2$($r$为半径),则半径分别为$\frac{a}{2}$、$\frac{b}{2}$、$\frac{c}{2}$,那么三个半圆的面积分别为$\frac{1}{2}\pi(\frac{a}{2})^2$、$\frac{1}{2}\pi(\frac{b}{2})^2$、$\frac{1}{2}\pi(\frac{c}{2})^2$。
已知较小的两个半圆的面积之和等于最大的半圆的面积,则可列出等式$\frac{1}{2}\pi(\frac{a}{2})^2 + \frac{1}{2}\pi(\frac{b}{2})^2 = \frac{1}{2}\pi(\frac{c}{2})^2$,化简该等式可得$a^2 + b^2 = c^2$。
根据勾股定理的逆定理:若一个三角形的三条边满足关系式$a^2 + b^2 = c^2$,则这个三角形是直角三角形,其中$c$为斜边。
所以这个三角形是直角三角形。
【答案】:B
设三个半圆的直径分别为$a$、$b$、$c$($c$为最大半圆的直径),根据圆的面积公式$S = \pi r^2$($r$为半径),则半径分别为$\frac{a}{2}$、$\frac{b}{2}$、$\frac{c}{2}$,那么三个半圆的面积分别为$\frac{1}{2}\pi(\frac{a}{2})^2$、$\frac{1}{2}\pi(\frac{b}{2})^2$、$\frac{1}{2}\pi(\frac{c}{2})^2$。
已知较小的两个半圆的面积之和等于最大的半圆的面积,则可列出等式$\frac{1}{2}\pi(\frac{a}{2})^2 + \frac{1}{2}\pi(\frac{b}{2})^2 = \frac{1}{2}\pi(\frac{c}{2})^2$,化简该等式可得$a^2 + b^2 = c^2$。
根据勾股定理的逆定理:若一个三角形的三条边满足关系式$a^2 + b^2 = c^2$,则这个三角形是直角三角形,其中$c$为斜边。
所以这个三角形是直角三角形。
【答案】:B
4. 如图,在$Rt△ABC和Rt△A'B'C'$中,$∠C= ∠C'= 90^{\circ }$,那么下列各条件中,不能使$Rt△ABC\cong Rt△A'B'C'$的是 (
B
)
答案:
【解析】:本题考查直角三角形全等的判定条件。
A选项给出的条件是斜边和一条直角边对应相等,这符合“HL”判定定理,所以能判定两个直角三角形全等。
C选项给出的条件是两条直角边对应相等,再加上直角这个公共条件,符合“SAS”判定定理,所以能判定两个直角三角形全等。
D选项给出的条件是一条直角边和它的邻角对应相等,再加上直角这个公共条件,符合“ASA”判定定理,所以能判定两个直角三角形全等。
B选项中给出的条件是$AB = B'C' = 5$(其中$AB$是$Rt\triangle ABC$的斜边,$B'C'$是$Rt\triangle A'B'C'$的一条直角边),$\angle A = \angle B' = 40^{\circ}$,这两个条件不满足全等三角形的任何一种判定方法,所以不能判定两个直角三角形全等。
【答案】:B
A选项给出的条件是斜边和一条直角边对应相等,这符合“HL”判定定理,所以能判定两个直角三角形全等。
C选项给出的条件是两条直角边对应相等,再加上直角这个公共条件,符合“SAS”判定定理,所以能判定两个直角三角形全等。
D选项给出的条件是一条直角边和它的邻角对应相等,再加上直角这个公共条件,符合“ASA”判定定理,所以能判定两个直角三角形全等。
B选项中给出的条件是$AB = B'C' = 5$(其中$AB$是$Rt\triangle ABC$的斜边,$B'C'$是$Rt\triangle A'B'C'$的一条直角边),$\angle A = \angle B' = 40^{\circ}$,这两个条件不满足全等三角形的任何一种判定方法,所以不能判定两个直角三角形全等。
【答案】:B
查看更多完整答案,请扫码查看


