4.如图,直线$y_{1}= x+b与y_{2}= kx-1$相交于点P,点P的横坐标为-1,则关于x的不等式$x+b>kx-1$的解集在数轴上可表示为 (
A
)
答案:
解:由图像可知,当$x > -1$时,直线$y_{1}=x+b$在直线$y_{2}=kx - 1$的上方,即$x + b > kx - 1$。
所以不等式$x + b > kx - 1$的解集为$x > -1$。
在数轴上表示为从$-1$出发向右的射线,且$-1$处为空心点。
观察选项,A选项符合。
答案:A
所以不等式$x + b > kx - 1$的解集为$x > -1$。
在数轴上表示为从$-1$出发向右的射线,且$-1$处为空心点。
观察选项,A选项符合。
答案:A
5.在全民健身环城越野赛中,甲、乙两选手的行程s(km)随时间t(h)变化的图象(全程)如图所示.有下列说法:①起跑后1h内,甲在乙的前面;②第1h两人都跑了10km;③甲比乙先到达终点;④两人都跑了20km.其中正确的说法有 (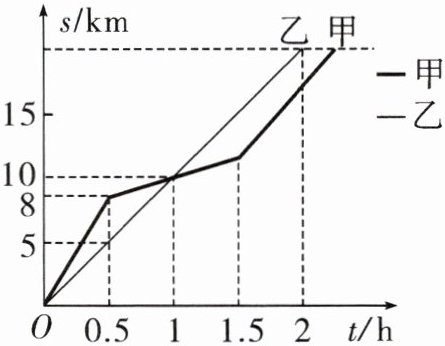
A.1个
B.2个
C.3个
D.4个
C
)
A.1个
B.2个
C.3个
D.4个
答案:
解:①起跑后1h内,甲的图象在乙的上方,故甲在乙前面,正确;
②当t=1h时,甲、乙的s值均为10km,正确;
③甲到达终点的时间大于2h,乙到达终点的时间为2h,故乙比甲先到达终点,错误;
④由图象可知,两人全程都跑了20km,正确。
正确的说法有①②④,共3个。
答案:C
②当t=1h时,甲、乙的s值均为10km,正确;
③甲到达终点的时间大于2h,乙到达终点的时间为2h,故乙比甲先到达终点,错误;
④由图象可知,两人全程都跑了20km,正确。
正确的说法有①②④,共3个。
答案:C
6.在正比例函数$y= -3mx$中,函数y的值随x值的增大而增大,则点P(m,5)在第
二
象限.
答案:
【解析】:
首先,我们分析正比例函数$y = -3mx$的单调性。
由题目条件知,当$x$增大时,$y$也增大,即函数是增函数。
在正比例函数中,当比例系数大于0时,函数是增函数;当比例系数小于0时,函数是减函数。
因此,我们有$-3m > 0$,
解这个不等式得到$m < 0$。
接下来,我们需要判断点$P(m,5)$所在的象限。
由于$m < 0$,且点$P$的纵坐标为5(正数),根据坐标系的性质,我们可以确定点$P(m,5)$在第二象限。
【答案】:
二
首先,我们分析正比例函数$y = -3mx$的单调性。
由题目条件知,当$x$增大时,$y$也增大,即函数是增函数。
在正比例函数中,当比例系数大于0时,函数是增函数;当比例系数小于0时,函数是减函数。
因此,我们有$-3m > 0$,
解这个不等式得到$m < 0$。
接下来,我们需要判断点$P(m,5)$所在的象限。
由于$m < 0$,且点$P$的纵坐标为5(正数),根据坐标系的性质,我们可以确定点$P(m,5)$在第二象限。
【答案】:
二
7.要从直线$y= \frac{4}{3}x$得到直线$y= \frac{4x+2}{3}$,就要将直线$y= \frac{4}{3}x$向
上
平移$\frac{2}{3}$
个单位.
答案:
解:将直线$y = \frac{4}{3}x$变形后的直线$y = \frac{4x + 2}{3}$化简为$y = \frac{4}{3}x + \frac{2}{3}$。
根据一次函数图像平移规律“上加下减”,对比$y = \frac{4}{3}x$与$y = \frac{4}{3}x + \frac{2}{3}$,可知是在$y = \frac{4}{3}x$的基础上向上平移了$\frac{2}{3}$个单位。
上;$\frac{2}{3}$
根据一次函数图像平移规律“上加下减”,对比$y = \frac{4}{3}x$与$y = \frac{4}{3}x + \frac{2}{3}$,可知是在$y = \frac{4}{3}x$的基础上向上平移了$\frac{2}{3}$个单位。
上;$\frac{2}{3}$
8.某公司在A,B两地分别有同型号的机器17台和15台,目前需要把这些机器中的18台运往甲地,14台运往乙地.从A,B两地运往甲、乙两地的费用(单位:元/台)如下表:
|地点|甲地|乙地|
|A地|600|500|
|B地|400|800|
(1)设从A地运往甲地x台,则从A地运往乙地
(2)当运送总费用为15800元时,请确定运送方案(即A,B两地运往甲、乙两地的机器各几台).
|地点|甲地|乙地|
|A地|600|500|
|B地|400|800|
(1)设从A地运往甲地x台,则从A地运往乙地
17 - x
台,从B地运往乙地x - 3
台.(结果用含x的代数式表示,且代数式化到最简)(2)当运送总费用为15800元时,请确定运送方案(即A,B两地运往甲、乙两地的机器各几台).
从A地运往甲地5台,运往乙地12台;从B地运往甲地13台,运往乙地2台。
答案:
【解析】:
(1) 本题主要考察线性方程的应用和代数表达式的简化。
设从A地运往甲地x台机器,则从A地运往乙地的机器数量为$17 - x$台(因为A地总共有17台机器)。
由于总共需要运往乙地14台机器,如果从A地运往乙地$17 - x$台,那么从B地运往乙地的机器数量就是$14 - (17 - x) = x - 3$台(但需要注意,这个数量不能为负,即$x \geq 3$)。
同时,总共需要运往甲地18台机器,如果从A地运往甲地x台,那么从B地运往甲地的机器数量就是$18 - x$台。
(2) 本题主要考察一元一次方程的解法和应用。
根据题目给出的运费标准,可以列出总运费的方程:
$600x + 500(17 - x) + 400(18 - x) + 800(x - 3) = 15800$
展开并整理得:
$600x + 8500 - 500x + 7200 - 400x + 800x - 2400 = 15800$
$500x + 13300 = 15800$
$500x = 2500$
$x = 5$
将$x = 5$代入之前的代数表达式中,得到具体的运送方案。
【答案】:
(1) 从A地运往乙地$17 - x$台,从B地运往乙地$x - 3$台。
(2) 当$x = 5$时,
从A地运往甲地5台,运往乙地$17 - 5 = 12$台;
从B地运往甲地$18 - 5 = 13$台,运往乙地$5 - 3 = 2$台。
(1) 本题主要考察线性方程的应用和代数表达式的简化。
设从A地运往甲地x台机器,则从A地运往乙地的机器数量为$17 - x$台(因为A地总共有17台机器)。
由于总共需要运往乙地14台机器,如果从A地运往乙地$17 - x$台,那么从B地运往乙地的机器数量就是$14 - (17 - x) = x - 3$台(但需要注意,这个数量不能为负,即$x \geq 3$)。
同时,总共需要运往甲地18台机器,如果从A地运往甲地x台,那么从B地运往甲地的机器数量就是$18 - x$台。
(2) 本题主要考察一元一次方程的解法和应用。
根据题目给出的运费标准,可以列出总运费的方程:
$600x + 500(17 - x) + 400(18 - x) + 800(x - 3) = 15800$
展开并整理得:
$600x + 8500 - 500x + 7200 - 400x + 800x - 2400 = 15800$
$500x + 13300 = 15800$
$500x = 2500$
$x = 5$
将$x = 5$代入之前的代数表达式中,得到具体的运送方案。
【答案】:
(1) 从A地运往乙地$17 - x$台,从B地运往乙地$x - 3$台。
(2) 当$x = 5$时,
从A地运往甲地5台,运往乙地$17 - 5 = 12$台;
从B地运往甲地$18 - 5 = 13$台,运往乙地$5 - 3 = 2$台。
查看更多完整答案,请扫码查看


