《2025年天舟文化精彩暑假团结出版社八年级数学湘教版》

6. 已知点$P(a+3,4-a),Q(2a,2b+3)关于y$轴对称,则$ab= $-1.

答案： 解：
∵点P(a+3,4-a)，Q(2a,2b+3)关于y轴对称，
∴横坐标互为相反数，纵坐标相等，
即$\begin{cases}a + 3 = -2a \\ 4 - a = 2b + 3\end{cases}$，
解第一个方程：$a + 2a = -3$，$3a = -3$，$a = -1$，
将$a = -1$代入第二个方程：$4 - (-1) = 2b + 3$，$5 = 2b + 3$，$2b = 2$，$b = 1$，
∴$ab = (-1)×1 = -1$。
-1

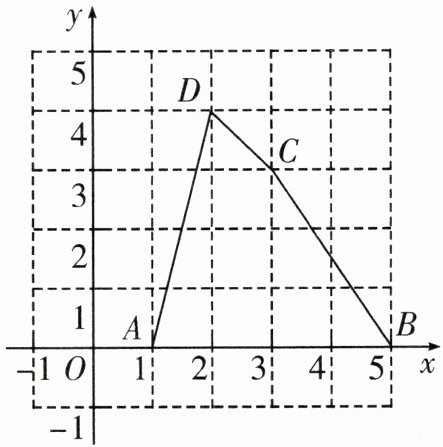
7. 如图,在平面直角坐标系中,四边形$ABCD的顶点坐标分别为A(1,0),B(5,0),C(3,3),D(2,4)$.
(1)求线段$AB$的长.
(2)求四边形$ABCD$的面积.

答案：
(1)解：因为A(1,0)，B(5,0)，所以AB的长为5-1=4。
(2)解：分别过点D、C作DE⊥x轴于E，CF⊥x轴于F。E(2,0)，F(3,0)。
S四边形ABCD=S△ADE+S梯形DEFC+S△CFB
S△ADE=1/2×(2-1)×4=2
S梯形DEFC=1/2×(4+3)×(3-2)=3.5
S△CFB=1/2×(5-3)×3=3
所以S四边形ABCD=2+3.5+3=8.5

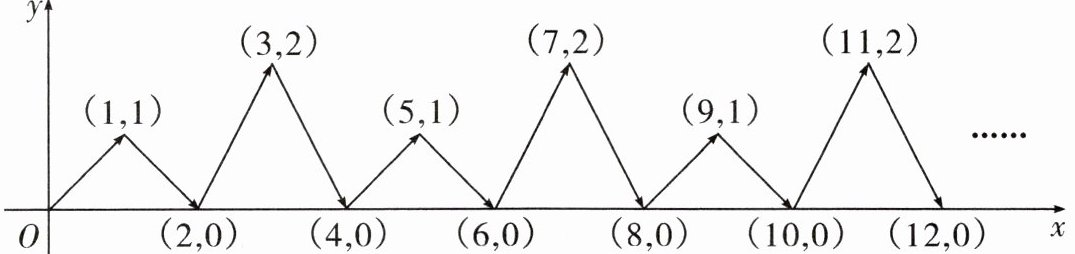
如图,动点$P$在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点$(1,1)$,第2次接着运动到点$(2,0)$,第3次接着运动到点$(3,2)$……按这样的运动规律,经过2023次运动后,求动点$P$的坐标.

答案： 【解析】：
本题我们需要先分析动点$P$的运动规律，然后找出横坐标和纵坐标的变化规律，最后根据规律求出经过2023次运动后动点$P$的坐标。
动点$P$的运动规律是：第1次从原点运动到点$(1,1)$，第2次接着运动到点$(2,0)$，第3次接着运动到点$(3,2)$，第4次接着运动到点$(4,0)$，第5次接着运动到点$(5,1)$，以此类推。
可以看出，动点$P$的横坐标就是运动次数，即第$n$次运动后，动点$P$的横坐标为$n$。
动点$P$的纵坐标呈现周期性变化，即$1,0,2,0$四个数一个循环。
我们可以通过计算$2023 ÷ 4 = 505\ldots\ldots 3$，余数为3，说明经过2023次运动后，动点$P$的纵坐标与第3次运动后的纵坐标相同，即2。
【答案】：
解：
∵第$n$次运动后，动点$P$的横坐标为$n$，
∴第2023次运动后，动点$P$的横坐标为2023，
∵动点$P$的纵坐标呈现周期性变化，即$1,0,2,0$四个数一个循环，
$2023 ÷ 4 = 505\ldots\ldots 3$，
∴经过2023次运动后，动点$P$的纵坐标与第3次运动后的纵坐标相同，即2，
∴经过2023次运动后，动点$P$的坐标为$(2023,2)$。