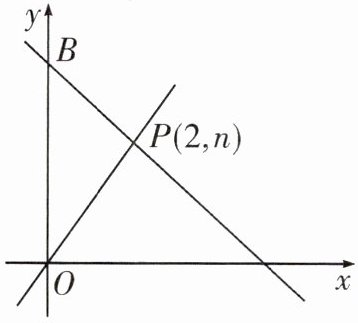
10. 如图所示,一次函数$y= -x+m$的图象和y轴交于点B,与正比例函数$y= \frac{3}{2}x的图象交于点P(2,n)$.
(1)求m和n的值.
(2)求$\triangle POB$的面积.
(1)求m和n的值.
(2)求$\triangle POB$的面积.

答案:
【解析】:
(1) 要求出m和n的值,由于点P(2,n)在正比例函数$y = \frac{3}{2}x$的图象上,可先通过代入求出n的值,再将点P的坐标代入一次函数$y = -x + m$求出m的值。
(2) 要求出$\triangle POB$的面积,需要知道点B的坐标,由于点B在一次函数$y = -x + m$的图象上且在y轴上,可令$x = 0$求出B点的坐标,进而得到OB的长度,再根据三角形面积公式求解。
【答案】:
(1) 因为点$P(2,n)$在正比例函数$y = \frac{3}{2}x$的图象上,所以将$x = 2$代入$y = \frac{3}{2}x$可得:
$n=\frac{3}{2}×2 = 3$
则点P的坐标为$(2,3)$。
又因为点$P(2,3)$在一次函数$y = -x + m$的图象上,将$x = 2$,$y = 3$代入$y = -x + m$可得:
$3=-2 + m$
解得$m = 5$。
所以,$m = 5$,$n = 3$。
(2) 由
(1)可知一次函数的解析式为$y = -x + 5$。
因为点B在一次函数$y = -x + 5$的图象上且在y轴上,令$x = 0$,可得$y = 5$,所以点B的坐标为$(0,5)$,则$OB = 5$。
点P的坐标为$(2,3)$,则P到y轴的距离(即$\triangle POB$中OB边上的高)为2。
根据三角形面积公式$S=\frac{1}{2}×底×高$,可得:
${S}_{\triangle POB}=\frac{1}{2}× OB× 2=\frac{1}{2}× 5× 2 = 5$
所以,$\triangle POB$的面积为5。
(1) 要求出m和n的值,由于点P(2,n)在正比例函数$y = \frac{3}{2}x$的图象上,可先通过代入求出n的值,再将点P的坐标代入一次函数$y = -x + m$求出m的值。
(2) 要求出$\triangle POB$的面积,需要知道点B的坐标,由于点B在一次函数$y = -x + m$的图象上且在y轴上,可令$x = 0$求出B点的坐标,进而得到OB的长度,再根据三角形面积公式求解。
【答案】:
(1) 因为点$P(2,n)$在正比例函数$y = \frac{3}{2}x$的图象上,所以将$x = 2$代入$y = \frac{3}{2}x$可得:
$n=\frac{3}{2}×2 = 3$
则点P的坐标为$(2,3)$。
又因为点$P(2,3)$在一次函数$y = -x + m$的图象上,将$x = 2$,$y = 3$代入$y = -x + m$可得:
$3=-2 + m$
解得$m = 5$。
所以,$m = 5$,$n = 3$。
(2) 由
(1)可知一次函数的解析式为$y = -x + 5$。
因为点B在一次函数$y = -x + 5$的图象上且在y轴上,令$x = 0$,可得$y = 5$,所以点B的坐标为$(0,5)$,则$OB = 5$。
点P的坐标为$(2,3)$,则P到y轴的距离(即$\triangle POB$中OB边上的高)为2。
根据三角形面积公式$S=\frac{1}{2}×底×高$,可得:
${S}_{\triangle POB}=\frac{1}{2}× OB× 2=\frac{1}{2}× 5× 2 = 5$
所以,$\triangle POB$的面积为5。
1. 小刚均匀地向一个容器注水,直到把容器注满.在注水过程中,水面高度h随时间t变化的规律如图所示(图中 OABC为折线),则这个容器的形状可能是 (
OABC为折线),则这个容器的形状可能是 (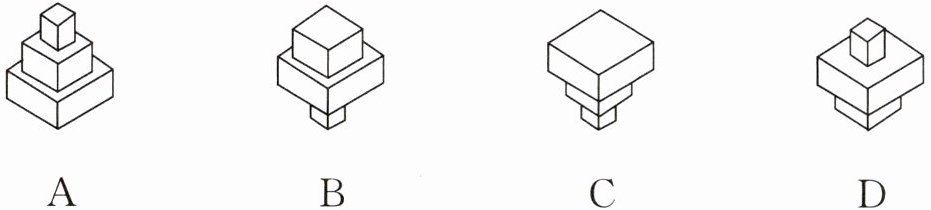
 OABC为折线),则这个容器的形状可能是 (
OABC为折线),则这个容器的形状可能是 (A
)
答案:
解:根据图像,OA段水面高度h随时间t增长较快,AB段增长变慢,BC段增长最快。由于注水速度均匀,容器横截面积越小,水面高度增长越快。因此容器形状应是下部分横截面积较小,中间横截面积变大,上部分横截面积最小。观察选项,符合此特征的是A。
答案:A
答案:A
2. 如图,在$\triangle ABC$中,$AC= BC$,有一动点P从点A出发,沿$A→C→B→A$匀速运动.则CP的长度s与时间 t之间的函数关系用图象描述大致是图中的 (
t之间的函数关系用图象描述大致是图中的 (
 t之间的函数关系用图象描述大致是图中的 (
t之间的函数关系用图象描述大致是图中的 (C
)
答案:
解:当点P从A向C运动时,CP长度s随时间t增大而减小,起点s=AC,终点s=0;
当点P从C向B运动时,CP长度s随时间t增大而增大,起点s=0,终点s=BC=AC;
当点P从B向A运动时,CP长度s先减小至最小值(C到AB的距离),再增大至AC,且最小值小于AC。
结合选项,符合上述变化的图象为C。
答案:C
当点P从C向B运动时,CP长度s随时间t增大而增大,起点s=0,终点s=BC=AC;
当点P从B向A运动时,CP长度s先减小至最小值(C到AB的距离),再增大至AC,且最小值小于AC。
结合选项,符合上述变化的图象为C。
答案:C
3. 一次函数$y= (m-1)x+(m-2)$的图象上有点M(x_1,y_1)和点N(x_2,y_2),且$x_1>x_2$.下列叙述正确的是 (
A.若该函数图象交y轴于正半轴,则$y_1<y_2$
B.该函数图象必经过点$(-1,-1)$
C.无论m为何值,该函数图象一定过第四象限
D.该函数图象向上平移一个单位后,会与x轴正半轴有交点
B
)A.若该函数图象交y轴于正半轴,则$y_1<y_2$
B.该函数图象必经过点$(-1,-1)$
C.无论m为何值,该函数图象一定过第四象限
D.该函数图象向上平移一个单位后,会与x轴正半轴有交点
答案:
【解析】:
本题考察一次函数的性质。
A. 若该函数图象交y轴于正半轴,则$m-2>0$,即$m>2$。
由于$x_1>x_2$,且斜率$m-1$的正负性不确定(因为$m>2$时,$m-1>0$,函数递增;但如果$m<1$,则$m-1<0$,函数递减),所以不能确定$y_1$和$y_2$的大小关系。故A选项错误。
B. 将$x=-1$代入函数$y=(m-1)x+(m-2)$,得到$y=-(m-1)+(m-2)=-1$,所以该函数图象必经过点$(-1,-1)$。故B选项正确。
C. 当$m>2$时,斜率$m-1>0$,且y轴上的截距$m-2>0$,此时函数图象不会进入第四象限。故C选项错误。
D. 函数图象向上平移一个单位后,新的函数为$y=(m-1)x+(m-1)$。
令$y=0$,解得$x=\frac{1-m}{m-1}=-1$(当$m \neq 1$时),即与x轴的交点为$(-1,0)$,不在正半轴上。
当$m=1$时,函数退化为常数函数$y=-1$,与x轴无交点。故D选项错误。
【答案】:
B
本题考察一次函数的性质。
A. 若该函数图象交y轴于正半轴,则$m-2>0$,即$m>2$。
由于$x_1>x_2$,且斜率$m-1$的正负性不确定(因为$m>2$时,$m-1>0$,函数递增;但如果$m<1$,则$m-1<0$,函数递减),所以不能确定$y_1$和$y_2$的大小关系。故A选项错误。
B. 将$x=-1$代入函数$y=(m-1)x+(m-2)$,得到$y=-(m-1)+(m-2)=-1$,所以该函数图象必经过点$(-1,-1)$。故B选项正确。
C. 当$m>2$时,斜率$m-1>0$,且y轴上的截距$m-2>0$,此时函数图象不会进入第四象限。故C选项错误。
D. 函数图象向上平移一个单位后,新的函数为$y=(m-1)x+(m-1)$。
令$y=0$,解得$x=\frac{1-m}{m-1}=-1$(当$m \neq 1$时),即与x轴的交点为$(-1,0)$,不在正半轴上。
当$m=1$时,函数退化为常数函数$y=-1$,与x轴无交点。故D选项错误。
【答案】:
B
4. 小亮每天从家去学校行走的路程为900m.某天他从家去上学时以30m/min的速度行走了前半程,为了不迟到他加快了速度,以45m/min的速度行走完剩下的路程.那么小亮行走的路程y(m)与他行走的时间t(min)$(t>15)$之间的函数关系正确的是 ( )
答案:
【解析】:
本题主要考查了分段函数的应用,需要根据不同时间段的速度来确定函数关系。
小亮每天从家去学校行走的总路程为900m。
他首先以30m/min的速度行走了前半程,即450m。
根据$\text{时间} = \frac{\text{路程}}{\text{速度}}$,
可得行走前半程所需的时间为$\frac{450}{30} = 15(min)$。
接着,他以45m/min的速度行走完剩下的450m。
同样根据$\text{时间} = \frac{\text{路程}}{\text{速度}}$,
可得行走后半程所需的时间为$\frac{450}{45} = 10(min)$。
因此,小亮行走的总时间为$15min + 10min = 25min$。
当$t > 15$时,小亮已经走完了前半程,正在以45m/min的速度行走后半程。
设小亮行走的时间为$t$ min($t > 15$),则他行走后半程的时间为$(t - 15)$ min。
在这段时间里,他行走的路程为$45(t - 15)$ m。
因此,小亮行走的总路程$y$与他行走的时间$t$之间的函数关系为:
$y = 450 + 45(t - 15) = 45t - 225$($15 < t \leq 25$),
由于小亮行走的总时间不超过25min,所以函数的定义域为$15 < t \leq 25$。
【答案】:
$y = 45t - 225$($15 < t \leq 25$)。
本题主要考查了分段函数的应用,需要根据不同时间段的速度来确定函数关系。
小亮每天从家去学校行走的总路程为900m。
他首先以30m/min的速度行走了前半程,即450m。
根据$\text{时间} = \frac{\text{路程}}{\text{速度}}$,
可得行走前半程所需的时间为$\frac{450}{30} = 15(min)$。
接着,他以45m/min的速度行走完剩下的450m。
同样根据$\text{时间} = \frac{\text{路程}}{\text{速度}}$,
可得行走后半程所需的时间为$\frac{450}{45} = 10(min)$。
因此,小亮行走的总时间为$15min + 10min = 25min$。
当$t > 15$时,小亮已经走完了前半程,正在以45m/min的速度行走后半程。
设小亮行走的时间为$t$ min($t > 15$),则他行走后半程的时间为$(t - 15)$ min。
在这段时间里,他行走的路程为$45(t - 15)$ m。
因此,小亮行走的总路程$y$与他行走的时间$t$之间的函数关系为:
$y = 450 + 45(t - 15) = 45t - 225$($15 < t \leq 25$),
由于小亮行走的总时间不超过25min,所以函数的定义域为$15 < t \leq 25$。
【答案】:
$y = 45t - 225$($15 < t \leq 25$)。
查看更多完整答案,请扫码查看


