《2025年天舟文化精彩暑假团结出版社八年级数学湘教版》

1. 下列各曲线中,表示y是x的函数的是 ( )

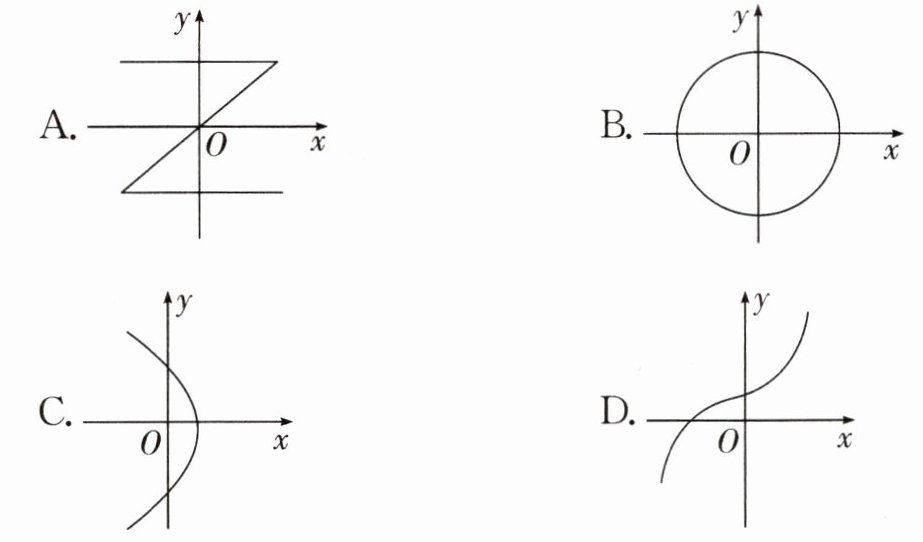
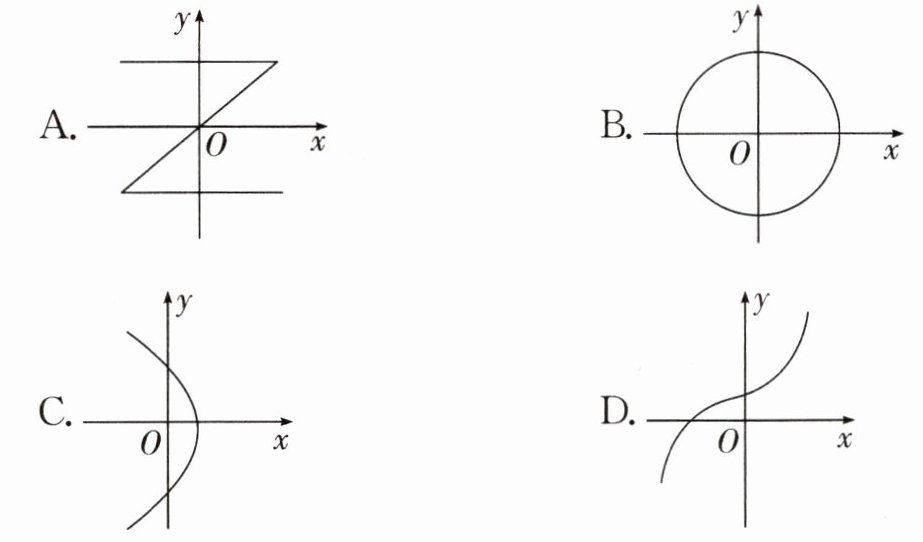
答案： D

2. 一根蜡烛长20cm,点燃后每小时燃烧5cm,燃烧时剩下的长度y(cm)与燃烧时间x(h)的函数关系可用图象表示为 (B)

答案： 【解析】：
本题考查实际问题与函数图象的关系，关键在于根据蜡烛的燃烧情况确定函数关系式以及自变量的取值范围。
步骤一：确定函数关系式
已知蜡烛长$20cm$，点燃后每小时燃烧$5cm$，燃烧时间设为$x$小时，剩下的长度设为$y$厘米。
因为蜡烛剩下的长度等于蜡烛原来的长度减去燃烧的长度，燃烧的长度为每小时燃烧的长度$5$厘米乘以燃烧时间$x$小时，所以可得函数关系式$y = 20 - 5x$。
步骤二：确定自变量$x$的取值范围
由于蜡烛的长度不能为负数，即$y\geq0$，那么$20 - 5x\geq0$，解这个不等式：
$20 - 5x\geq0$，移项可得$5x\leq20$，两边同时除以$5$，解得$x\leq4$。
又因为燃烧时间$x\geq0$，所以自变量$x$的取值范围是$0\leq x\leq4$。
步骤三：分析函数图象
函数$y = 20 - 5x$是一次函数，其中$k=-5\lt0$，所以$y$随$x$的增大而减小。
当$x = 0$时，$y = 20 - 5×0 = 20$；当$x = 4$时，$y = 20 - 5×4 = 0$。
结合自变量$x$的取值范围$0\leq x\leq4$，可知函数图象是一条线段，起点为$(0, 20)$，终点为$(4, 0)$。
逐一分析选项：
选项A：图象中$x = 4$时，$y$的值大于$0$，不符合当$x = 4$时，$y = 0$的情况，所以该选项错误。
选项B：该图象是一条从$(0, 20)$到$(4, 0)$的线段，符合$y = 20 - 5x(0\leq x\leq4)$的函数图象，所以该选项正确。
选项C：此图象在$x\geq0$时，$y$的值始终为$20$，表示蜡烛不燃烧，与题目中蜡烛每小时燃烧$5cm$的条件不符，所以该选项错误。
选项D：该图象中$x$的取值范围没有限制，而实际中$x$的取值范围是$0\leq x\leq4$，所以该选项错误。
综上，答案是B。
【答案】：B。