5. 一个正方形的边长为3cm,它的各边边长减少xcm后,得到的新正方形的周长为ycm,则用含x的代数式表示y为____.

答案:
【解析】:
本题考查正方形的周长公式及代数式的表示。
首先,原正方形的边长为$3cm$。当各边边长减少$xcm$后,新的边长变为$(3-x)cm$。
正方形的周长是其边长的四倍,所以新的正方形的周长$y$可以表示为:
$y = 4 × (3-x) = 4(3-x) = 12 - 4x$。
【答案】:
$y = 12 - 4x$。
本题考查正方形的周长公式及代数式的表示。
首先,原正方形的边长为$3cm$。当各边边长减少$xcm$后,新的边长变为$(3-x)cm$。
正方形的周长是其边长的四倍,所以新的正方形的周长$y$可以表示为:
$y = 4 × (3-x) = 4(3-x) = 12 - 4x$。
【答案】:
$y = 12 - 4x$。
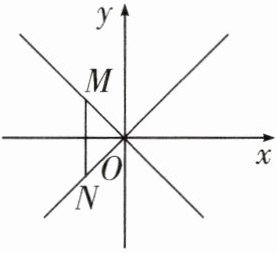
6. 如图,在平面直角坐标系中,点M是直线$y= -x$上的动点,过点M作$MN\perp x$轴,交直线$y= x$于点N.当$MN\leqslant8$时,设点M的横坐标为m,则m的取值范围为
$-4 \leq m \leq 4$
.
答案:
解:
∵点M在直线$y = -x$上,横坐标为m,
∴点M坐标为$(m, -m)$。
∵MN⊥x轴交直线$y = x$于点N,
∴点N横坐标为m,代入$y = x$得N$(m, m)$。
∴$MN = |m - (-m)| = |2m|$。
∵$MN \leq 8$,
∴$|2m| \leq 8$,即$|m| \leq 4$。
∴$-4 \leq m \leq 4$。
$-4 \leq m \leq 4$
∵点M在直线$y = -x$上,横坐标为m,
∴点M坐标为$(m, -m)$。
∵MN⊥x轴交直线$y = x$于点N,
∴点N横坐标为m,代入$y = x$得N$(m, m)$。
∴$MN = |m - (-m)| = |2m|$。
∵$MN \leq 8$,
∴$|2m| \leq 8$,即$|m| \leq 4$。
∴$-4 \leq m \leq 4$。
$-4 \leq m \leq 4$
7. 已知$y_1与x^2$成正比例,$y_2与x-2$成正比例,且$y= y_1-y_2$.当$x= 1$时,$y= 0$;当$x= -3$时,$y= 4$.求y与x之间的函数关系式.
答案:
【解析】:
本题主要考查正比例函数的性质以及待定系数法求函数解析式。
首先,根据题目条件,$y_1$ 与 $x^2$ 成正比例,$y_2$ 与 $x-2$ 成正比例,因此可以设 $y_1 = ax^2$,$y_2 = b(x - 2)$。
由于 $y = y_1 - y_2$,代入 $y_1$ 和 $y_2$ 的表达式,得到 $y = ax^2 - b(x - 2)$。
接下来,利用题目给出的两个点 $(1, 0)$ 和 $(-3, 4)$ 来求解 $a$ 和 $b$。
将点 $(1, 0)$ 代入 $y = ax^2 - b(x - 2)$,得到 $0 = a \cdot 1^2 - b(1 - 2)$,即 $0 = a + b$。
将点 $(-3, 4)$ 代入 $y = ax^2 - b(x - 2)$,得到 $4 = a \cdot (-3)^2 - b(-3 - 2)$,即 $4 = 9a + 5b$。
现在有一个包含 $a$ 和 $b$ 的二元一次方程组:
$\begin{cases}a + b = 0 \\9a + 5b = 4\end{cases}$
解这个方程组,得到 $a = 1$,$b = -1$。
最后,将 $a$ 和 $b$ 的值代入 $y = ax^2 - b(x - 2)$,得到 $y = x^2 + (x - 2)$,即 $y = x^2 + x - 2$。
【答案】:
解:设 $y_1 = ax^2$,$y_2 = b(x - 2)$,则 $y = y_1 - y_2 = ax^2 - b(x - 2)$。
根据题目条件,当 $x = 1$ 时,$y = 0$;当 $x = -3$ 时,$y = 4$。
代入得:
$\begin{cases}a + b = 0 \\9a + 5b = 4\end{cases}$
解方程组得 $a = 1$,$b = -1$。
因此,$y$ 与 $x$ 之间的函数关系式为 $y = x^2 + x - 2$。
本题主要考查正比例函数的性质以及待定系数法求函数解析式。
首先,根据题目条件,$y_1$ 与 $x^2$ 成正比例,$y_2$ 与 $x-2$ 成正比例,因此可以设 $y_1 = ax^2$,$y_2 = b(x - 2)$。
由于 $y = y_1 - y_2$,代入 $y_1$ 和 $y_2$ 的表达式,得到 $y = ax^2 - b(x - 2)$。
接下来,利用题目给出的两个点 $(1, 0)$ 和 $(-3, 4)$ 来求解 $a$ 和 $b$。
将点 $(1, 0)$ 代入 $y = ax^2 - b(x - 2)$,得到 $0 = a \cdot 1^2 - b(1 - 2)$,即 $0 = a + b$。
将点 $(-3, 4)$ 代入 $y = ax^2 - b(x - 2)$,得到 $4 = a \cdot (-3)^2 - b(-3 - 2)$,即 $4 = 9a + 5b$。
现在有一个包含 $a$ 和 $b$ 的二元一次方程组:
$\begin{cases}a + b = 0 \\9a + 5b = 4\end{cases}$
解这个方程组,得到 $a = 1$,$b = -1$。
最后,将 $a$ 和 $b$ 的值代入 $y = ax^2 - b(x - 2)$,得到 $y = x^2 + (x - 2)$,即 $y = x^2 + x - 2$。
【答案】:
解:设 $y_1 = ax^2$,$y_2 = b(x - 2)$,则 $y = y_1 - y_2 = ax^2 - b(x - 2)$。
根据题目条件,当 $x = 1$ 时,$y = 0$;当 $x = -3$ 时,$y = 4$。
代入得:
$\begin{cases}a + b = 0 \\9a + 5b = 4\end{cases}$
解方程组得 $a = 1$,$b = -1$。
因此,$y$ 与 $x$ 之间的函数关系式为 $y = x^2 + x - 2$。
在平面直角坐标系xOy中,点$P(x_0,y_0)到直线Ax+By+C= 0(A^2+B^2\neq0)的距离公式为d= \frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}$.
例如,求点$P(1,3)到直线4x+3y-3= 0$的距离.
解:由直线$4x+3y-3= 0$,知$A= 4,B= 3,C= -3$.
所以$P(1,3)到直线4x+3y-3= 0的距离d= \frac{|4×1+3×3-3|}{\sqrt{4^2+3^2}}= 2$.
根据以上材料,解决下列问题:
(1)求点$P_1(0,0)到直线3x-4y-5= 0$的距离.
(2)若点$P_2(1,0)到直线x+y+C= 0的距离为\sqrt{2}$,求实数C的值.
例如,求点$P(1,3)到直线4x+3y-3= 0$的距离.
解:由直线$4x+3y-3= 0$,知$A= 4,B= 3,C= -3$.
所以$P(1,3)到直线4x+3y-3= 0的距离d= \frac{|4×1+3×3-3|}{\sqrt{4^2+3^2}}= 2$.
根据以上材料,解决下列问题:
(1)求点$P_1(0,0)到直线3x-4y-5= 0$的距离.
(2)若点$P_2(1,0)到直线x+y+C= 0的距离为\sqrt{2}$,求实数C的值.
答案:
【解析】:
本题主要考察点到直线的距离公式的应用。
(1)对于点$P_1(0,0)$到直线$3x-4y-5= 0$的距离,可以直接将点$P_1$的坐标和直线的系数代入距离公式进行计算。
(2)对于点$P_2(1,0)$到直线$x+y+C= 0$的距离为$\sqrt{2}$,可以先将点$P_2$的坐标和直线的系数代入距离公式,然后根据题目给出的距离值,解出实数$C$的值。
【答案】:
(1)解:由直线$3x-4y-5= 0$,知$A= 3$,$B= -4$,$C= -5$。
所以$P_1(0,0)$到直线$3x-4y-5= 0$的距离$d$为:
$d= \frac{|3×0 - 4×0 - 5|}{\sqrt{3^2 + (-4)^2}} = \frac{|-5|}{5} = 1$;
(2)解:由直线$x+y+C= 0$,知$A= 1$,$B= 1$,$C$为未知数。
因为$P_2(1,0)$到直线$x+y+C= 0$的距离为$\sqrt{2}$,
所以有:
$\frac{|1×1 + 1×0 + C|}{\sqrt{1^2 + 1^2}} = \sqrt{2}$
即:
$\frac{|1 + C|}{\sqrt{2}} = \sqrt{2}$
$|1 + C| = 2$
解得:
$C= 1$ 或 $C= -3$。
本题主要考察点到直线的距离公式的应用。
(1)对于点$P_1(0,0)$到直线$3x-4y-5= 0$的距离,可以直接将点$P_1$的坐标和直线的系数代入距离公式进行计算。
(2)对于点$P_2(1,0)$到直线$x+y+C= 0$的距离为$\sqrt{2}$,可以先将点$P_2$的坐标和直线的系数代入距离公式,然后根据题目给出的距离值,解出实数$C$的值。
【答案】:
(1)解:由直线$3x-4y-5= 0$,知$A= 3$,$B= -4$,$C= -5$。
所以$P_1(0,0)$到直线$3x-4y-5= 0$的距离$d$为:
$d= \frac{|3×0 - 4×0 - 5|}{\sqrt{3^2 + (-4)^2}} = \frac{|-5|}{5} = 1$;
(2)解:由直线$x+y+C= 0$,知$A= 1$,$B= 1$,$C$为未知数。
因为$P_2(1,0)$到直线$x+y+C= 0$的距离为$\sqrt{2}$,
所以有:
$\frac{|1×1 + 1×0 + C|}{\sqrt{1^2 + 1^2}} = \sqrt{2}$
即:
$\frac{|1 + C|}{\sqrt{2}} = \sqrt{2}$
$|1 + C| = 2$
解得:
$C= 1$ 或 $C= -3$。
查看更多完整答案,请扫码查看


