5. 如图,在$△BAC$中,$AC= 5,BC= 12,AB= 13$,CD 是 AB 边上的中线,则$CD= $
6.5
.
答案:
【解析】:本题可先根据勾股定理的逆定理判断$\triangle BAC$的形状,再根据直角三角形斜边中线定理求出$CD$的长度。
步骤一:判断$\triangle BAC$的形状
勾股定理的逆定理为:若一个三角形的三条边满足关系式$a^2 + b^2 = c^2$,则这个三角形是直角三角形,其中$c$为最长边。
在$\triangle BAC$中,$AC = 5$,$BC = 12$,$AB = 13$,分别计算$AC^{2}+BC^{2}$与$AB^{2}$的值:
$AC^{2}+BC^{2}=5^{2}+12^{2}=25 + 144 = 169$
$AB^{2}=13^{2}=169$
因为$AC^{2}+BC^{2}=AB^{2}$,所以$\triangle BAC$是直角三角形,且$\angle C = 90^{\circ}$。
步骤二:求$CD$的长度
直角三角形斜边中线定理为:直角三角形斜边的中线等于斜边的一半。
已知$CD$是$AB$边上的中线,即$D$为$AB$的中点,$AB = 13$,根据上述定理可得:
$CD=\frac{1}{2}AB=\frac{1}{2}×13 = 6.5$
【答案】:$6.5$
步骤一:判断$\triangle BAC$的形状
勾股定理的逆定理为:若一个三角形的三条边满足关系式$a^2 + b^2 = c^2$,则这个三角形是直角三角形,其中$c$为最长边。
在$\triangle BAC$中,$AC = 5$,$BC = 12$,$AB = 13$,分别计算$AC^{2}+BC^{2}$与$AB^{2}$的值:
$AC^{2}+BC^{2}=5^{2}+12^{2}=25 + 144 = 169$
$AB^{2}=13^{2}=169$
因为$AC^{2}+BC^{2}=AB^{2}$,所以$\triangle BAC$是直角三角形,且$\angle C = 90^{\circ}$。
步骤二:求$CD$的长度
直角三角形斜边中线定理为:直角三角形斜边的中线等于斜边的一半。
已知$CD$是$AB$边上的中线,即$D$为$AB$的中点,$AB = 13$,根据上述定理可得:
$CD=\frac{1}{2}AB=\frac{1}{2}×13 = 6.5$
【答案】:$6.5$
6. 如图,已知在$△ABC$中,$AB= 10,AC= 8,BC= 6$,DE 是 AC 的垂直平分线,DE 交 AB 于点 D,交 AC 于点 E.连接 CD,则$CD= $
6.8
.
答案:
解:
∵DE是AC的垂直平分线,
∴CD=AD。
设CD=AD=x,则BD=AB-AD=10-x。
∵AC=8,BC=6,AB=10,
且$6^{2}+8^{2}=36 + 64=100=10^{2}$,
∴$△ABC$是直角三角形,$∠ACB=90^{\circ}$。
在$Rt△BCD$中,由勾股定理得:$CD^{2}=BC^{2}+BD^{2}$,
即$x^{2}=6^{2}+(10 - x)^{2}$,
解得$x=6.8$,即$CD=6.8$。
6.8
∵DE是AC的垂直平分线,
∴CD=AD。
设CD=AD=x,则BD=AB-AD=10-x。
∵AC=8,BC=6,AB=10,
且$6^{2}+8^{2}=36 + 64=100=10^{2}$,
∴$△ABC$是直角三角形,$∠ACB=90^{\circ}$。
在$Rt△BCD$中,由勾股定理得:$CD^{2}=BC^{2}+BD^{2}$,
即$x^{2}=6^{2}+(10 - x)^{2}$,
解得$x=6.8$,即$CD=6.8$。
6.8
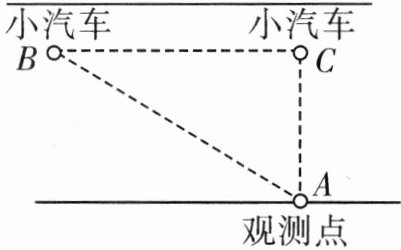
7. 如图,一辆小汽车在某限速为 70 km/h 的直道上行驶,某一时刻刚好行驶到距车速检测仪 A(观测点)30 m 的 C 处,过了 2 s 后,测得小汽车所在位置 B 与车速检测仪间的距离为 50 m,且$∠ACB= 90^{\circ }$.问:这辆小汽车超速了吗? (参考数据:$1m/s= 3.6km/h$)

答案:
【解析】:本题可先根据勾股定理求出小汽车在$2s$内行驶的距离,再根据速度公式求出小汽车的速度,最后将速度单位换算为$km/h$并与限速比较,判断是否超速。
步骤一:求出$BC$的长度
在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = 30m$,$AB = 50m$。
根据勾股定理$AB^{2}=AC^{2}+BC^{2}$,可得$BC=\sqrt{AB^{2}-AC^{2}}$。
将$AC = 30m$,$AB = 50m$代入上式,可得:
$BC=\sqrt{50^{2}-30^{2}}=\sqrt{(50 + 30)(50 - 30)}=\sqrt{80×20}=\sqrt{1600}= 40m$
步骤二:求出小汽车的速度
已知小汽车从$C$处行驶到$B$处用了$2s$,根据速度公式$v = \frac{s}{t}$(其中$v$表示速度,$s$表示路程,$t$表示时间),可得小汽车的速度为:
$v=\frac{BC}{2}=\frac{40}{2}= 20m/s$
步骤三:将速度单位换算为$km/h$
已知$1m/s = 3.6km/h$,则$20m/s$换算为$km/h$为:
$20×3.6 = 72km/h$
步骤四:判断小汽车是否超速
已知该直道限速为$70km/h$,而小汽车的速度为$72km/h$,因为$72\gt 70$,所以这辆小汽车超速了。
【答案】:这辆小汽车超速了。
步骤一:求出$BC$的长度
在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = 30m$,$AB = 50m$。
根据勾股定理$AB^{2}=AC^{2}+BC^{2}$,可得$BC=\sqrt{AB^{2}-AC^{2}}$。
将$AC = 30m$,$AB = 50m$代入上式,可得:
$BC=\sqrt{50^{2}-30^{2}}=\sqrt{(50 + 30)(50 - 30)}=\sqrt{80×20}=\sqrt{1600}= 40m$
步骤二:求出小汽车的速度
已知小汽车从$C$处行驶到$B$处用了$2s$,根据速度公式$v = \frac{s}{t}$(其中$v$表示速度,$s$表示路程,$t$表示时间),可得小汽车的速度为:
$v=\frac{BC}{2}=\frac{40}{2}= 20m/s$
步骤三:将速度单位换算为$km/h$
已知$1m/s = 3.6km/h$,则$20m/s$换算为$km/h$为:
$20×3.6 = 72km/h$
步骤四:判断小汽车是否超速
已知该直道限速为$70km/h$,而小汽车的速度为$72km/h$,因为$72\gt 70$,所以这辆小汽车超速了。
【答案】:这辆小汽车超速了。
查看更多完整答案,请扫码查看


