《2025年天舟文化精彩暑假团结出版社八年级数学湘教版》

7. 如图,在$\triangle ABC$中,$∠ACB= 90^{\circ }$,BC的垂直平分线DE交BC于点D,交AB于点E,点F在DE的延长线上,且$AF= CE= AE$.
(1)求证：四边形ACEF是平行四边形.
(2)当$∠B$满足什么条件时,四边形ACEF是菱形？请说明理由.

答案： 【解析】：
本题主要考查了平行四边形的判定、菱形的判定、线段垂直平分线的性质、直角三角形的性质等知识点。
（1）要证明四边形$ACEF$是平行四边形，需要证明$AF// CE$且$AF = CE$，可通过证明$AF$和$CE$所在的三角形全等，得到对应边相等和对应角相等，进而得出四边形$ACEF$是平行四边形。
（2）要使四边形$ACEF$是菱形，需要邻边相等，结合（1）中平行四边形的性质，通过分析$\angle B$的度数，利用直角三角形的性质得到边的关系，从而判断四边形$ACEF$是否为菱形。
【答案】：
（1）证明：
∵$DE$是$BC$的垂直平分线，
∴$EB = EC$，$\angle BDE = 90^{\circ}$，
∵$\angle ACB = 90^{\circ}$，
∴$DE// AC$，
∵$AF = AE = CE$，
∴$\angle F = \angle AEF$，$\angle B = \angle BCE$，$\angle AEF = \angle BED$，
∵$\angle B + \angle BAC = 90^{\circ}$，$\angle BCE + \angle ACE = 90^{\circ}$，
∴$\angle BAC = \angle ACE$，
∵$AE = CE$，
∴$\angle EAC = \angle ACE$，
∴$\angle EAC = \angle BAC$，
∵$DE// AC$，
∴$\angle BED = \angle EAC$，
∴$\angle F = \angle BED = \angle B$，
∵$\angle F + \angle FAE = 180^{\circ}$，$\angle B + \angle BAC = 90^{\circ}$，$\angle F = \angle B$，
∴$\angle FAE = \angle BAC + \angle EAC = 90^{\circ}$，
∴$AF// CE$，
∵$AF = CE$，
∴四边形$ACEF$是平行四边形。
（2）当$\angle B = 30^{\circ}$时，四边形$ACEF$是菱形。
理由如下：
∵$\angle B = 30^{\circ}$，$\angle ACB = 90^{\circ}$，
∴$AC = \frac{1}{2}AB$，
∵$DE$是$BC$的垂直平分线，
∴$BE = CE$，
∵$\angle B = 30^{\circ}$，
∴$\angle BCE = \angle B = 30^{\circ}$，$\angle BAC = 60^{\circ}$，
∵$\angle ACB = 90^{\circ}$，
∴$\angle ACE = \angle ACB - \angle BCE = 60^{\circ}$，
∵$AE = CE$，
∴$\triangle ACE$是等边三角形，
∴$AC = CE$，
∵四边形$ACEF$是平行四边形，
∴四边形$ACEF$是菱形。

在一次数学实践探究活动中,小强用两条直线把$□ ABCD$分割成四部分,使含有一组对顶角的两个图形全等.

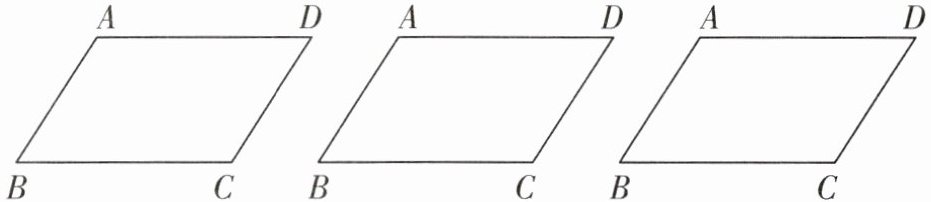
(1)请你分别在图中的三个平行四边形中画出满足小强分割要求的不同直线.
(2)根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的四部分的直线有几组？
(3)由上述实验操作过程,你发现所画的两条直线有什么规律？

答案： 【解析】：
(1) 根据平行四边形的性质，中心对称的特点，以及全等图形的定义，我们可以确定，经过平行四边形的中心的两条直线，可以将平行四边形分成四部分，且含有一组对顶角的两个图形全等。具体地，我们可以在图中的三个平行四边形中分别画出这样的直线。
(2) 由于平行四边形是中心对称图形，对称中心为两条对角线的交点，因此，经过这个交点的任意两条直线，都可以将平行四边形分割成满足全等关系的四部分。这样的直线有无数组。
(3) 由上述实验操作过程，我们可以发现所画的两条直线必须经过平行四边形的对称中心，即两条对角线的交点。
【答案】：
(1)图略（经过平行四边形的中心的两条直线，将平行四边形分成四部分，且含有一组对顶角的两个图形全等）；
(2)无数组；
(3)过平行四边形的对称中心（或两条对角线的交点）。