《2025年天舟文化精彩暑假团结出版社八年级数学湘教版》

5. 如图,O 是$△ABC$内一点,且点 O 到三边 AB,BC,CA 的距离$OF= OD= OE$.若$∠BAC= 70^{\circ }$,则$∠BOC$的度数是 (D)
A.$35^{\circ}$
B.$145^{\circ}$
C.$55^{\circ}$
D.$125^{\circ}$

答案： 【解析】：本题可根据角平分线的判定定理得出点$O$是三个角的平分线的交点，再利用三角形内角和定理求出$\angle ABC + \angle ACB$的度数，进而求出$\angle OBC + \angle OCB$的度数，最后根据三角形内角和定理求出$\angle BOC$的度数。
步骤一：根据角平分线的判定定理确定点$O$的位置
角平分线的判定定理为：到角的两边距离相等的点在角的平分线上。
已知点$O$到三边$AB$，$BC$，$CA$的距离$OF = OD = OE$，其中$OF\perp AB$，$OD\perp BC$，$OE\perp AC$，所以点$O$在$\angle BAC$、$\angle ABC$、$\angle ACB$的平分线上，即$AO$、$BO$、$CO$分别是$\angle BAC$、$\angle ABC$、$\angle ACB$的平分线。
步骤二：求出$\angle ABC + \angle ACB$的度数
在$\triangle ABC$中，根据三角形内角和定理：三角形的内角和等于$180^{\circ}$，已知$\angle BAC = 70^{\circ}$，则可得：
$\angle ABC + \angle ACB = 180^{\circ} - \angle BAC = 180^{\circ} - 70^{\circ} = 110^{\circ}$
步骤三：求出$\angle OBC + \angle OCB$的度数
因为$BO$、$CO$分别是$\angle ABC$、$\angle ACB$的平分线，所以$\angle OBC = \frac{1}{2}\angle ABC$，$\angle OCB = \frac{1}{2}\angle ACB$，则：
$\angle OBC + \angle OCB = \frac{1}{2}(\angle ABC + \angle ACB) = \frac{1}{2}×110^{\circ} = 55^{\circ}$
步骤四：求出$\angle BOC$的度数
在$\triangle BOC$中，根据三角形内角和定理，可得：
$\angle BOC = 180^{\circ} - (\angle OBC + \angle OCB) = 180^{\circ} - 55^{\circ} = 125^{\circ}$
【答案】：D

6. 如图,OP 平分$∠AOB,∠AOP= 15^{\circ },PC// OA,PD⊥OA$于点 D,$PC= 4$,则$PD= $2.

答案： 【解析】：本题可根据角平分线的性质以及平行线的性质来求解$PD$的长度。
步骤一：根据角平分线的性质和平行线的性质确定相关角度和线段关系
已知$OP$平分$\angle AOB$，$\angle AOP = 15^{\circ}$，根据角平分线的定义：从一个角的顶点出发，把这个角分成相等的两个角的射线叫做这个角的平分线，可得$\angle AOB = 2\angle AOP = 2×15^{\circ} = 30^{\circ}$。
因为$PC// OA$，根据两直线平行，同位角相等，可得$\angle CPO = \angle AOP = 15^{\circ}$。
步骤二：过点$P$作$PE\perp OB$于点$E$
由于$OP$平分$\angle AOB$，$PD\perp OA$，$PE\perp OB$，根据角平分线的性质：角平分线上的点到角两边的距离相等，可知$PD = PE$。
步骤三：在$Rt\triangle PCE$中，利用$30^{\circ}$所对的直角边是斜边的一半求出$PE$的长度
因为$\angle AOB = 30^{\circ}$，$PC// OA$，所以$\angle PCE = \angle AOB = 30^{\circ}$（两直线平行，同位角相等）。
在$Rt\triangle PCE$中，$\angle PCE = 30^{\circ}$，$PC = 4$，根据在直角三角形中，$30^{\circ}$所对的直角边等于斜边的一半，可得$PE=\frac{1}{2}PC=\frac{1}{2}×4 = 2$。
步骤四：根据$PD = PE$求出$PD$的长度
因为$PD = PE$，$PE = 2$，所以$PD = 2$。
【答案】：$2$

7. 如图,在四边形 ABCD 中,$CB= CD,∠ABC= ∠ADC= 90^{\circ },∠BAC= 35^{\circ }$,则$∠BCD$的度数为$110^{\circ}$.

答案： 【解析】：本题考查了全等三角形的判定与性质，以及四边形内角和定理。
由题可知，$\angle ABC=\angle ADC=90^{\circ}$，且$CB=CD$，$AC=AC$（公共边）。
根据$HL$全等条件，可以证明$\triangle ABC\cong\triangle ADC$。
由于$\triangle ABC\cong\triangle ADC$，所以对应角相等，即$\angle ACB=\angle ACD$。
已知$\angle BAC=35^{\circ}$，在直角三角形$ABC$中，$\angle ACB=180^{\circ}-90^{\circ}-35^{\circ}=55^{\circ}$。
因此，$\angle ACD=\angle ACB=55^{\circ}$。
所以，$\angle BCD=\angle ACB+\angle ACD=55^{\circ}+55^{\circ}=110^{\circ}$。
【答案】：$110^{\circ}$。

8. 如图,AB,CD 相交于点 O,且$BD= BO,CA= CO$,E,F,M 分别是 OD,OA,BC 的中点.求证:$ME= MF$.

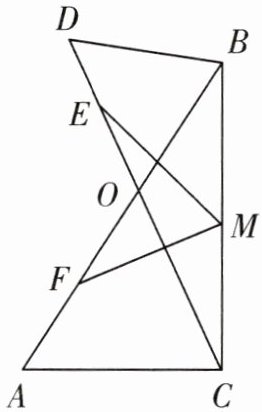
答案： 证明：连接BE, CF。
∵BD=BO，E是OD中点，
∴BE⊥OD（等腰三角形三线合一），
∴∠BEC=90°。
∵M是BC中点，
∴ME=1/2BC（直角三角形斜边中线等于斜边一半）。
∵CA=CO，F是OA中点，
∴CF⊥OA（等腰三角形三线合一），
∴∠CFB=90°。
∵M是BC中点，
∴MF=1/2BC（直角三角形斜边中线等于斜边一半）。
∴ME=MF。

9. 如图,四边形 ABCD 中,$AD= 4,BC= 1,∠A= 30^{\circ },∠B= 90^{\circ },∠ADC= 120^{\circ }$,求 CD 的长.

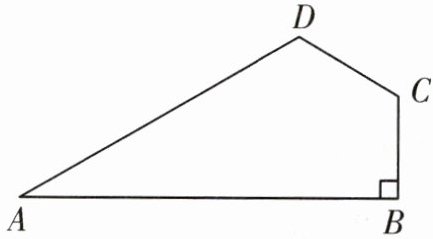
答案： 解：延长AD、BC交于点E。
在Rt△ABE中，∠A=30°，设CD=x，∠ADC=120°，则∠EDC=60°。
设CD=x，在△EDC中，∠E=60°，∠EDC=60°，故△EDC为等边三角形，EC=CD=DE=x。
AE=AD+DE=4+x，BE=BC+CE=1+x。
在Rt△ABE中，∠A=30°，则BE=AE·tan30°，即1+x=(4+x)·(√3/3)。
解得x= (√3 - 3)/ (1 - √3/3) = 1。
CD=1。