5. 如图,直线 l 过正方形 ABCD 的顶点 B,点 A,C 到直线 l 的距离分别是1 和 2,则该正方形的边长是 (
A.$\sqrt {3}$
B.$\sqrt {5}$
C.3
D.$\sqrt {7}$
B
)A.$\sqrt {3}$
B.$\sqrt {5}$
C.3
D.$\sqrt {7}$
答案:
解:过点A作AE⊥直线l于E,过点C作CF⊥直线l于F,则AE=1,CF=2,∠AEB=∠CFB=90°。
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABE+∠CBF=90°。
∵∠ABE+∠BAE=90°,
∴∠BAE=∠CBF。
在△ABE和△BCF中,
∠AEB=∠BFC,∠BAE=∠CBF,AB=BC,
∴△ABE≌△BCF(AAS),
∴BE=CF=2。
在Rt△ABE中,AB²=AE²+BE²=1²+2²=5,
∴AB=√5。
答案:B
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABE+∠CBF=90°。
∵∠ABE+∠BAE=90°,
∴∠BAE=∠CBF。
在△ABE和△BCF中,
∠AEB=∠BFC,∠BAE=∠CBF,AB=BC,
∴△ABE≌△BCF(AAS),
∴BE=CF=2。
在Rt△ABE中,AB²=AE²+BE²=1²+2²=5,
∴AB=√5。
答案:B
6. 如图,在$□ABCD$中,已知$∠A= 70^{\circ },DC= DB$,则$∠CDB$的度数为____.
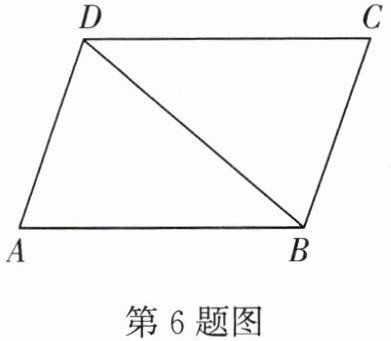

40°
答案:
解:
∵四边形ABCD是平行四边形,
∴∠C=∠A=70°,AB=DC,AD=BC,AB//DC,AD//BC。
∵DC=DB,
∴DB=DC,
∴△DBC是等腰三角形,∠DBC=∠C=70°。
在△DBC中,∠CDB=180°-∠C-∠DBC=180°-70°-70°=40°。
40°
∵四边形ABCD是平行四边形,
∴∠C=∠A=70°,AB=DC,AD=BC,AB//DC,AD//BC。
∵DC=DB,
∴DB=DC,
∴△DBC是等腰三角形,∠DBC=∠C=70°。
在△DBC中,∠CDB=180°-∠C-∠DBC=180°-70°-70°=40°。
40°
7. 如图,直线 MN 过$□ABCD$的中心点 O,交 AD 于点 M,交 BC 于点 N.已知$S_{□ABCD}= 4$,则$S_{阴影}= $
1
.
答案:
解:
∵四边形ABCD是平行四边形,O是中心点,
∴OA=OC,AD//BC,
∴∠OAM=∠OCN,∠OMA=∠ONC,
∴△OAM≌△OCN(AAS),
∴S△OAM=S△OCN,
∴S阴影=S△OAB,
∵O是平行四边形ABCD的中心,
∴S△OAB=1/4S□ABCD=1/4×4=1,
故S阴影=1。
答案:1
∵四边形ABCD是平行四边形,O是中心点,
∴OA=OC,AD//BC,
∴∠OAM=∠OCN,∠OMA=∠ONC,
∴△OAM≌△OCN(AAS),
∴S△OAM=S△OCN,
∴S阴影=S△OAB,
∵O是平行四边形ABCD的中心,
∴S△OAB=1/4S□ABCD=1/4×4=1,
故S阴影=1。
答案:1
8. 如图,点 A,F,C,D 在同一直线上,点 B 和点 E 分别在直线 AD 的两侧,且$AB= DE,∠A= ∠D,AF= DC$. 求证:四边形 BCEF 是平行四边形.
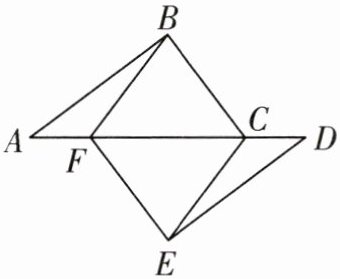

答案:
【解析】:本题主要考察全等三角形的判定和性质以及平行四边形的判定,首先通过已知条件证明三角形全等,得出对应边相等即$BC=EF$,再通过平行线的判定得出$BC// EF$,最后根据一组对边平行且相等的四边形是平行四边形得出结论。
【答案】:证明:
在$\bigtriangleup ABC$和$\bigtriangleup DEF$中,
$\left\{\begin{matrix}AB=DE,\\\angle A=\angle D,\\AF=DC.\end{matrix}\right.$
由于$AF = DC$,所以$AF + FC = DC + FC$,即$AC = DF$。
所以$\left\{\begin{matrix}AB=DE,\\\angle A=\angle D,\\AC = DF.\end{matrix}\right.$
所以$\bigtriangleup ABC\cong\bigtriangleup DEF(SAS)$。
所以$BC = EF,\angle ACB=\angle DFE$,
所以$BC// EF$,
所以四边形$BCEF$是平行四边形(一组对边平行且相等的四边形是平行四边形)。
【答案】:证明:
在$\bigtriangleup ABC$和$\bigtriangleup DEF$中,
$\left\{\begin{matrix}AB=DE,\\\angle A=\angle D,\\AF=DC.\end{matrix}\right.$
由于$AF = DC$,所以$AF + FC = DC + FC$,即$AC = DF$。
所以$\left\{\begin{matrix}AB=DE,\\\angle A=\angle D,\\AC = DF.\end{matrix}\right.$
所以$\bigtriangleup ABC\cong\bigtriangleup DEF(SAS)$。
所以$BC = EF,\angle ACB=\angle DFE$,
所以$BC// EF$,
所以四边形$BCEF$是平行四边形(一组对边平行且相等的四边形是平行四边形)。
9. 如图,在四边形 ABCD 中,$∠A= ∠BCD= 90^{\circ },BC= CD,CE⊥AD$,垂足为 E. 求证:$AE= CE.$
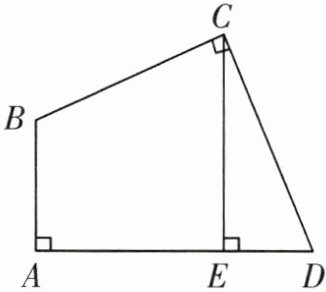

答案:
【解析】:本题可通过构造全等三角形来证明$AE = CE$。观察到四边形$ABCD$中有两个直角$\angle A = \angle BCD = 90^{\circ}$,且$BC = CD$,$CE\perp AD$,可尝试通过作辅助线,利用全等三角形的判定定理来证明。
过点$C$作$CF\perp AB$,交$AB$的延长线于点$F$。
此时需要证明$\triangle CDE$和$\triangle CBF$全等,进而得到$CE = CF$,再结合已知条件证明$AE = CE$。
【答案】:证明:
过点$C$作$CF\perp AB$,交$AB$的延长线于点$F$。
∵$CE\perp AD$,$CF\perp AB$,$\angle A = 90^{\circ}$,
∴四边形$AECF$是矩形(有三个角是直角的四边形是矩形)。
∴$\angle F = 90^{\circ}$,$\angle FCE = 90^{\circ}$(矩形的四个角都是直角)。
∵$\angle BCD = 90^{\circ}$,
∴$\angle BCF+\angle FCD = \angle DCE+\angle FCD = 90^{\circ}$。
∴$\angle BCF = \angle DCE$(同角的余角相等)。
∵在$\triangle CDE$和$\triangle CBF$中,
$\begin{cases}\angle DCE=\angle BCF \\ \angle DEC=\angle F = 90^{\circ} \\ BC = CD\end{cases}$
∴$\triangle CDE\cong\triangle CBF(AAS)$。
∴$CE = CF$(全等三角形的对应边相等)。
∵四边形$AECF$是矩形,且$CE = CF$,
∴四边形$AECF$是正方形(一组邻边相等的矩形是正方形)。
∴$AE = CE$(正方形的四条边都相等)。
过点$C$作$CF\perp AB$,交$AB$的延长线于点$F$。
此时需要证明$\triangle CDE$和$\triangle CBF$全等,进而得到$CE = CF$,再结合已知条件证明$AE = CE$。
【答案】:证明:
过点$C$作$CF\perp AB$,交$AB$的延长线于点$F$。
∵$CE\perp AD$,$CF\perp AB$,$\angle A = 90^{\circ}$,
∴四边形$AECF$是矩形(有三个角是直角的四边形是矩形)。
∴$\angle F = 90^{\circ}$,$\angle FCE = 90^{\circ}$(矩形的四个角都是直角)。
∵$\angle BCD = 90^{\circ}$,
∴$\angle BCF+\angle FCD = \angle DCE+\angle FCD = 90^{\circ}$。
∴$\angle BCF = \angle DCE$(同角的余角相等)。
∵在$\triangle CDE$和$\triangle CBF$中,
$\begin{cases}\angle DCE=\angle BCF \\ \angle DEC=\angle F = 90^{\circ} \\ BC = CD\end{cases}$
∴$\triangle CDE\cong\triangle CBF(AAS)$。
∴$CE = CF$(全等三角形的对应边相等)。
∵四边形$AECF$是矩形,且$CE = CF$,
∴四边形$AECF$是正方形(一组邻边相等的矩形是正方形)。
∴$AE = CE$(正方形的四条边都相等)。
查看更多完整答案,请扫码查看


